题目内容
12. 如图所示,水平传送带由电动机带动以恒定的速度v顺时针匀速转动,某时刻一个质量为m的小物块在传送带上由静止释放,小物块与传送带间的动摩擦因数为μ,小物块在滑下传送带之前已与传送带的速度相同,对于小物块从静止释放到与传送带的速度相同这一过程中,下列说法正确的是( )
如图所示,水平传送带由电动机带动以恒定的速度v顺时针匀速转动,某时刻一个质量为m的小物块在传送带上由静止释放,小物块与传送带间的动摩擦因数为μ,小物块在滑下传送带之前已与传送带的速度相同,对于小物块从静止释放到与传送带的速度相同这一过程中,下列说法正确的是( )| A. | 电动机多做的功为$\frac{1}{2}$mv2 | |
| B. | 小物块在传送带上的划痕长为$\frac{{v}^{2}}{μg}$ | |
| C. | 传送带克服摩擦力做的功为$\frac{1}{2}$mv2 | |
| D. | 电动机增加的功率为μmgv |
分析 由于物块与传送带间有相对位移,物块对传送带做功与传送带对物块做功并不相等.系统摩擦生热等于系统克服摩擦力做的总功.物体在传送带上运动时,物体和传送带要发生相对滑动,所以电动机多做的功一部分转化成了物体的动能另一部分就是增加了相同的内能.根据牛顿第二定律和运动学公式求得物块与传送带间的相对位移,即得到划痕长度.结合功能关系分析.
解答 解:A、设物块匀加速运动的时间为t,则物块与传送带相对位移大小为:
△x=vt-$\frac{v}{2}t$=$\frac{1}{2}$vt
此过程中物块的位移为:x物=$\frac{v}{2}t$=$\frac{1}{2}$vt
则有:△x=x物.
物块运动过程中,只有摩擦力对它做功,根据动能定理得:摩擦力对物块做的功为:
Wf=fx物=$\frac{1}{2}m{v}^{2}$-0=$\frac{1}{2}$mv2.
系统摩擦生热为:Q=f•△x=fx物=$\frac{1}{2}$mv2.
电动机多做的功转化成了物体的动能和系统的内能,所以电动机多做的功为:W机=$\frac{1}{2}m{v}^{2}$+Q=mv2.故A错误.
B、物块匀加速运动的加速度为:a=$\frac{μmg}{m}$=μg
匀加速运动的时间为:t=$\frac{v}{a}$=$\frac{v}{μg}$,所以有:△x=$\frac{1}{2}$vt=$\frac{{v}^{2}}{2μg}$,则物块在传送带上的划痕长为$\frac{{v}^{2}}{2μg}$,故B错误.
C、传送带克服摩擦力做功为:Wf带=μmg•vt=μmg•v•$\frac{v}{μg}$=mv2.故C错误.
D、电动机增加的功率即为克服摩擦力做功的功率,大小为:P=fv=μmgv,故D正确.
故选:D
点评 解决本题的关键知道物体在传送带上发生相对运动时的运动规律,以及知道能量的转化,知道电动机多做的功等于物体动能的增加和摩擦产生的内能之和.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案| A. | 平抛运动是匀变速曲线运动 | |
| B. | 平抛运动的初速度越大,落地时间就越长 | |
| C. | 做圆周运动的物体所受合外力就是向心力 | |
| D. | 做匀速圆周运动的物体的加速度是不变的 |
| A. | 物体上升过程经历的时间大于下落过程经历的时间 | |
| B. | 物体上升过程动能的减少量大于下落过程动能的增加量 | |
| C. | 物体上升过程机械能的减少量大于下落过程机械能的减少量 | |
| D. | 物体上升过程重力的平均功率小于下落过程重力的平均功率 |
| A. | 手对物体做功20J | B. | 合外力对物体做功12J | ||
| C. | 合外力对物体做功2J | D. | 物体克服重力做功20J |
| A. | 如果用紫光照射某种金属能发生光电效应,改用绿光照射该金属一定也能发生光电效应 | |
| B. | α粒子散射实验中少数α粒子发生了较大偏转,这是卢瑟福猜想原子核式结构模型的主要依据之一 | |
| C. | 贝克勒尔通过对天然放射现象的研究,发现了原子中存在原子核 | |
| D. | 根据波尔理论,氢原子的核外电子由较高能级跃迁到较低能级时,要释放一定频率的光子,同时电子的动能增大,原子的电势能减小 |
 作为第十三届全运人的东道主,双人10米台为天津跳水队的重点项目.跳台跳水可简化为如下的运动过程,运动员从跳台上斜向上跳起,一段时间后落入水中,如图所示.不计空气阻力,下列说法正确的是( )
作为第十三届全运人的东道主,双人10米台为天津跳水队的重点项目.跳台跳水可简化为如下的运动过程,运动员从跳台上斜向上跳起,一段时间后落入水中,如图所示.不计空气阻力,下列说法正确的是( )| A. | 运动员在空中上升过程中处于超重状态 | |
| B. | 运动员在空中运动到最高点时速度为0 | |
| C. | 运动员在空中运动过程中机械能守恒 | |
| D. | 入水过程中,水对运动员的作用力大于运动员对水的作用力 |
| A. | $\frac{v}{4}\sqrt{\frac{2h}{g}}$ | B. | $\frac{2v}{3}\sqrt{\frac{2h}{g}}$ | C. | $\frac{4v}{3}\sqrt{\frac{2h}{g}}$ | D. | 4v$\sqrt{\frac{2h}{g}}$ |
| A. | 若汽车以恒定的功率运动,那么牵引力与速度成反比 | |
| B. | 若汽车起动后作匀加速运动,那么速度的最大值vm=$\frac{{P}_{额}}{f}$ | |
| C. | 汽车作匀速运动的速度与发动机实际功率成正比 | |
| D. | 汽车作匀速运动时,发动机实际功率一定等于额定功率 |
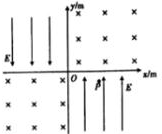 在xOy平面内存在着如图所示的匀强电场和匀强磁场,其中二、四象限内电场方向与y轴平行且大小相等、方向相反,一、三象限内磁场方向垂直xOy平面向里、磁感应强度大小B=0.2T,一带正电的粒子质量m=2×10-32kg、电荷量q=1×10-30C,从第四象限内的P(0.3m,-0.1m)点由静止释放,粒子垂直y轴方向进入第二象限,粒子重力不计,求:
在xOy平面内存在着如图所示的匀强电场和匀强磁场,其中二、四象限内电场方向与y轴平行且大小相等、方向相反,一、三象限内磁场方向垂直xOy平面向里、磁感应强度大小B=0.2T,一带正电的粒子质量m=2×10-32kg、电荷量q=1×10-30C,从第四象限内的P(0.3m,-0.1m)点由静止释放,粒子垂直y轴方向进入第二象限,粒子重力不计,求: