题目内容
7. 如图所示,一等腰三角形玻璃砖OAB的顶角∠AOB=2θ,其中0°<θ<90°,玻璃砖的折射率为n=2.要使一束从AB面垂直射入的光在OA和OB两个面都发生全反射,仅考虑光束第一次经OA面反射和第一次经OB面反射的情况,求θ的取值范围.
如图所示,一等腰三角形玻璃砖OAB的顶角∠AOB=2θ,其中0°<θ<90°,玻璃砖的折射率为n=2.要使一束从AB面垂直射入的光在OA和OB两个面都发生全反射,仅考虑光束第一次经OA面反射和第一次经OB面反射的情况,求θ的取值范围.
分析 先根据临界角公式sinC=$\frac{1}{n}$,求全反射临界角C.当光线在OA面和OB面的入射角都大于等于C时都能发生全反射,结合全反射条件和几何关系求解.
解答 解:由临界角公式:$sinC=\frac{1}{n}$
解得:C=30°
如图所示,在OA面上入射角 α=90°-θ≥30°
可得:θ≤60°
在OB面:β=90°-(180°-3θ)≥30°
可得:θ≥40°
所以:40°≤θ≤60°
讨论:若θ较小,则在OA面可能出现如图2所示情况,则:
γ=180°-3θ-90°≥30°
可得:θ≤20°
综上可得:0°<θ≤20°或40°≤θ≤60°.
答:θ的取值范围为0°<θ≤20°或40°≤θ≤60°.
点评 本题关键要理解全反射现象及其产生的条件,知道临界角其实是入射角,能灵活几何关系分析入射角的范围.

练习册系列答案
相关题目
17.对于一定质量的理想气体,下列说法正确的是( )
| A. | 当两个分子间的距离为r0(平衡位置)时,分子势能最小 | |
| B. | 布朗运动反映了花粉小颗粒内部分子的无规则运动 | |
| C. | 一定量的气体,在体积不变时,单位时间内分子平均碰撞器壁的次数随着温度降低而减小 | |
| D. | 液晶的光学性质不随温度、电磁作用变化而改变 | |
| E. | 一定质量的气体,在绝热压缩的过程中,内能一定增大 |
15. 如图,垂直于纸面向里的匀强磁场分布在正方形abcd区域内,O点是cd边的中点.一个带正电的粒子从O点沿纸面以垂直于cd边的速度射入正方形内,仅在磁场力的作用下,经过时间t0刚好从c点射出磁场.现设法使该带电粒子从O点沿纸面内与Od成30°的方向,以大小不同的速率射入正方形内,下列说法中正确的是( )
如图,垂直于纸面向里的匀强磁场分布在正方形abcd区域内,O点是cd边的中点.一个带正电的粒子从O点沿纸面以垂直于cd边的速度射入正方形内,仅在磁场力的作用下,经过时间t0刚好从c点射出磁场.现设法使该带电粒子从O点沿纸面内与Od成30°的方向,以大小不同的速率射入正方形内,下列说法中正确的是( )
 如图,垂直于纸面向里的匀强磁场分布在正方形abcd区域内,O点是cd边的中点.一个带正电的粒子从O点沿纸面以垂直于cd边的速度射入正方形内,仅在磁场力的作用下,经过时间t0刚好从c点射出磁场.现设法使该带电粒子从O点沿纸面内与Od成30°的方向,以大小不同的速率射入正方形内,下列说法中正确的是( )
如图,垂直于纸面向里的匀强磁场分布在正方形abcd区域内,O点是cd边的中点.一个带正电的粒子从O点沿纸面以垂直于cd边的速度射入正方形内,仅在磁场力的作用下,经过时间t0刚好从c点射出磁场.现设法使该带电粒子从O点沿纸面内与Od成30°的方向,以大小不同的速率射入正方形内,下列说法中正确的是( )| A. | 若该带电粒子在磁场中经历的时间是$\frac{5}{3}$t0,则它一定是从cd边射出磁场 | |
| B. | 若该带电粒子在磁场中经历的时间是$\frac{1}{2}$t0,则它一定是从ad边射出磁场 | |
| C. | 若该带电粒子在磁场中经历的时间是$\frac{1}{4}$t0,则它一定是从ab边射出磁场 | |
| D. | 若该带电粒子在磁场中经历的时间是t0,则它一定是从bc边射出磁场 |
2. 北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中两颗工作卫星1和2均绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,如图所示.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.下列判断中正确的是( )
北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中两颗工作卫星1和2均绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,如图所示.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.下列判断中正确的是( )
 北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中两颗工作卫星1和2均绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,如图所示.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.下列判断中正确的是( )
北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中两颗工作卫星1和2均绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,如图所示.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.下列判断中正确的是( )| A. | 两颗卫星的向心力大小一定相等 | |
| B. | 卫星1加速后即可追上卫星2 | |
| C. | 两颗卫星的向心加速度大小均为$\frac{{{R^2}g}}{r^2}$ | |
| D. | 卫星l由位置A运动至位置B所需的时间可能为$\frac{7πr}{3R}\sqrt{\frac{r}{g}}$ |
16. 一端装有定滑轮的粗糙斜面体放在地面上,A、B两物体通过细绳连接,并处于静止状态(不计绳的质量和绳与滑轮间的摩擦),如图所示.现用水平力F作用于物体B上,缓慢拉开一小角度,此过程中斜面体与物体A仍然静止.则下列说法正确的是( )
一端装有定滑轮的粗糙斜面体放在地面上,A、B两物体通过细绳连接,并处于静止状态(不计绳的质量和绳与滑轮间的摩擦),如图所示.现用水平力F作用于物体B上,缓慢拉开一小角度,此过程中斜面体与物体A仍然静止.则下列说法正确的是( )
 一端装有定滑轮的粗糙斜面体放在地面上,A、B两物体通过细绳连接,并处于静止状态(不计绳的质量和绳与滑轮间的摩擦),如图所示.现用水平力F作用于物体B上,缓慢拉开一小角度,此过程中斜面体与物体A仍然静止.则下列说法正确的是( )
一端装有定滑轮的粗糙斜面体放在地面上,A、B两物体通过细绳连接,并处于静止状态(不计绳的质量和绳与滑轮间的摩擦),如图所示.现用水平力F作用于物体B上,缓慢拉开一小角度,此过程中斜面体与物体A仍然静止.则下列说法正确的是( )| A. | 水平力F保持不变 | B. | 斜面对物体A的作用力一定变大 | ||
| C. | 斜面对物体A的摩擦力一定变大 | D. | 斜面体所受地面的支持力一定不变 |
 如图所示,一竖直倒放的U型管内用水银封住A、B两段气体,大气压强为75cmHg,则PA=65cmHg,PB=75cmHg.
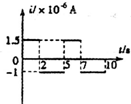
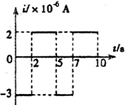
如图所示,一竖直倒放的U型管内用水银封住A、B两段气体,大气压强为75cmHg,则PA=65cmHg,PB=75cmHg.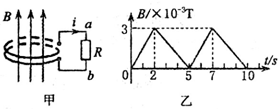 如图甲,匝数n=2的金属线圈(电阻不计)围成的面积为10cm2,线圈与R=2Ω的电阻连接,置于竖直向上、均匀分布的磁场中.磁场与线圈平面垂直,磁感应强度为B.B-t关系如图乙,规定感应电流i从a经过R到b的方向为正方向.忽略线圈的自感影响.则下列i-t关系图正确的是( )
如图甲,匝数n=2的金属线圈(电阻不计)围成的面积为10cm2,线圈与R=2Ω的电阻连接,置于竖直向上、均匀分布的磁场中.磁场与线圈平面垂直,磁感应强度为B.B-t关系如图乙,规定感应电流i从a经过R到b的方向为正方向.忽略线圈的自感影响.则下列i-t关系图正确的是( )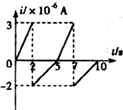
 如图所示为一上表面水平的透明玻璃半球,在其下面有一水平放置的光屏.两束关于中心轴OO′对称的激光束从半球上表面垂直射入玻璃半球,恰能从球面射出.当光屏距半球上表面h1=40cm时,从球面折射出的两束光线汇聚于光屏与OO′轴的交点,当光屏距上表面h2=80cm时,在光屏上形成半径r=40cm的圆形光斑.求该半球形玻璃的折射率.
如图所示为一上表面水平的透明玻璃半球,在其下面有一水平放置的光屏.两束关于中心轴OO′对称的激光束从半球上表面垂直射入玻璃半球,恰能从球面射出.当光屏距半球上表面h1=40cm时,从球面折射出的两束光线汇聚于光屏与OO′轴的交点,当光屏距上表面h2=80cm时,在光屏上形成半径r=40cm的圆形光斑.求该半球形玻璃的折射率.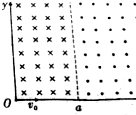 如图所示,在第一象限内,0<x≤a的区域中有垂直于纸面向里的匀强磁场,已知磁感应强度的大小为B1;x>a的区域中有垂直于纸面向外的匀强磁场,在原点O处有一小孔,一束质量为m、电荷量为q带正电的粒子,沿着x轴方向以不同的速率经小孔射入磁场,且速率最大的粒子在0<x≤a区域内运动的时候转过的圆心角为60°,它最终从x轴离开磁场时速度方向与x轴负方向的夹角为30°,不计粒子重力,求:
如图所示,在第一象限内,0<x≤a的区域中有垂直于纸面向里的匀强磁场,已知磁感应强度的大小为B1;x>a的区域中有垂直于纸面向外的匀强磁场,在原点O处有一小孔,一束质量为m、电荷量为q带正电的粒子,沿着x轴方向以不同的速率经小孔射入磁场,且速率最大的粒子在0<x≤a区域内运动的时候转过的圆心角为60°,它最终从x轴离开磁场时速度方向与x轴负方向的夹角为30°,不计粒子重力,求: