题目内容
17.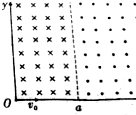 如图所示,在第一象限内,0<x≤a的区域中有垂直于纸面向里的匀强磁场,已知磁感应强度的大小为B1;x>a的区域中有垂直于纸面向外的匀强磁场,在原点O处有一小孔,一束质量为m、电荷量为q带正电的粒子,沿着x轴方向以不同的速率经小孔射入磁场,且速率最大的粒子在0<x≤a区域内运动的时候转过的圆心角为60°,它最终从x轴离开磁场时速度方向与x轴负方向的夹角为30°,不计粒子重力,求:
如图所示,在第一象限内,0<x≤a的区域中有垂直于纸面向里的匀强磁场,已知磁感应强度的大小为B1;x>a的区域中有垂直于纸面向外的匀强磁场,在原点O处有一小孔,一束质量为m、电荷量为q带正电的粒子,沿着x轴方向以不同的速率经小孔射入磁场,且速率最大的粒子在0<x≤a区域内运动的时候转过的圆心角为60°,它最终从x轴离开磁场时速度方向与x轴负方向的夹角为30°,不计粒子重力,求:(1)从y轴离开磁场的粒子,在y轴上的出射点到O点的最大距离;
(2)x>a区域磁感应强度的大小B2;
(3)在x>a区域中所有粒子轨迹的最高点的y坐标的取值范围.
分析 (1)打到y轴上的粒子均沿半个圆周运动,离O最远的粒子轨迹刚好与两磁场交界线相切,画出轨迹即可求解;
(2)根据速度最大的粒子在0<x≤a中运动时间求出其对应的圆心角,根据几何关系求出半径,通过x>a的区域后,离开磁场时速度方向与x轴负方向的夹角为30°,画出运动的轨迹,确定圆心的位置,根据几何关系即可求得轨迹的半径,然后又半径公式即可求出;
(3)恰好进入x>a的区域的粒子向上的位移最大,画出粒子运动轨迹,根据几何关系最高点的y坐标的取值范围.
解答 解:(1)打到y轴上的粒子均沿半个圆周运动,离O最远的粒子轨迹刚好与两磁场交界线相切(如图轨迹①)
则R=a
所以:ymax=2R=2a
(2)速度最大的粒子在0<x≤a中运动的偏转角是60°,其对应的圆心角为60°,所以R′=$\frac{a}{sin60°}=\frac{2\sqrt{3}}{3}a$
通过x>a的区域后,最终从x轴离开磁场时速度方向与x轴负方向的夹角为30°,画出运动的轨迹如图(如图轨迹②)
由几何关系可知,对应的圆心角为210°,
由图中几何关系可得轨迹的半径:r•co30°+rcos60°=DE,
$DE=R′-R′cos60°=\frac{1}{2}R′=\frac{\sqrt{3}}{3}a$
所以:$r=\frac{2DE}{1+\sqrt{3}}$=$\frac{2a}{3+\sqrt{3}}$
由洛伦兹力提供向心力得:$q{v}_{m}•{B}_{1}=\frac{m{v}_{m}^{2}}{R′}$
又$q{v}_{m}•{B}_{2}=\frac{m{v}_{m}^{2}}{r}$
所以:${B}_{2}=(1+\sqrt{3}){B}_{1}$
(3)恰好穿过x=a的粒子运动的方向向上,其轨迹如图中③.
该粒子在x<a的范围内的半径为R,则:$R=\frac{mv}{q{B}_{1}}$
该粒子在x>a的范围内的半径为R″,则:$R″=\frac{mv}{q{B}_{2}}$
联立得:$R″=\frac{a}{1+\sqrt{3}}$
所以粒子到达的最高点的高度:${h}_{max}=R+R″=\frac{2+\sqrt{3}}{1+\sqrt{3}}a$
当粒子的速度最大时,粒子到达的最高点是所有粒子中最低的,其高度:hmin=R′(1-cos60°)+r(1-cos60°)=$\frac{2+\sqrt{3}}{3+\sqrt{3}}a$
所以,在x>a区域中所有粒子轨迹的最高点的y坐标的取值范围是:$\frac{2+\sqrt{3}}{3+\sqrt{3}}a≤y≤\frac{2+\sqrt{3}}{1+\sqrt{3}}a$
答:(1)y轴上粒子射出点到原点O的最大距离为2a;
(2)x>a区域磁感应强度的大小是$(1+\sqrt{3}){B}_{1}$;
(3)在x>a区域中所有粒子轨迹的最高点的y坐标的取值范围是$\frac{2+\sqrt{3}}{3+\sqrt{3}}a≤y≤\frac{2+\sqrt{3}}{1+\sqrt{3}}a$.
点评 该题考查带电粒子在磁场中的运动,带电粒子在磁场中运动的题目解题步骤为:定圆心、画轨迹、求半径,同时还利用圆弧的对称性来帮助解题.


| A. | 1.5V | B. | 1.7V | C. | 1V | D. | 1.4V |
 一列简谐横波沿x轴传播,t=0时的波形如图示,质点A与质点B相距1m,A点速度沿y轴正方向;t=0.02s时,质点A第二次到达正向最大位移处,由此可知( )
一列简谐横波沿x轴传播,t=0时的波形如图示,质点A与质点B相距1m,A点速度沿y轴正方向;t=0.02s时,质点A第二次到达正向最大位移处,由此可知( )| A. | 此波沿x轴负方向传播 | |
| B. | 此波的传播速度为125m/s | |
| C. | 从t=0时起,经过0.04 s,质点A沿波传播方向迁移了5m | |
| D. | 在t=0.04 s时,质点B处在平衡位置,速度沿y轴负方向 | |
| E. | 能与该波发生干涉的横波的频率一定为62.5Hz |
| A. | α粒子散射实验是估算原子核半径最简单的方法之一 | |
| B. | 光子像其他粒子一样,不但具有能量,也具有质量 | |
| C. | 玻尔理论认为原子的能量是连续的,电子的轨道半径是不连续的 | |
| D. | 光照到某金属上不能发生光电效应,是因为该光波长太短 |
 如图所示,一等腰三角形玻璃砖OAB的顶角∠AOB=2θ,其中0°<θ<90°,玻璃砖的折射率为n=2.要使一束从AB面垂直射入的光在OA和OB两个面都发生全反射,仅考虑光束第一次经OA面反射和第一次经OB面反射的情况,求θ的取值范围.
如图所示,一等腰三角形玻璃砖OAB的顶角∠AOB=2θ,其中0°<θ<90°,玻璃砖的折射率为n=2.要使一束从AB面垂直射入的光在OA和OB两个面都发生全反射,仅考虑光束第一次经OA面反射和第一次经OB面反射的情况,求θ的取值范围.

 页岩气是从页岩层中开采出来的天然气,主要成分为甲烷,被公认是洁净的能源.
页岩气是从页岩层中开采出来的天然气,主要成分为甲烷,被公认是洁净的能源.