题目内容
5. 如图所示,半径分别为R=1m,r=0.5m的甲、乙两圆形轨道放置在同一竖直面内,斜面与水平轨道由一小段圆弧轨道相连,两圆形轨道之间由一个水平轨道CD相连,小球与CD段间的动摩擦因数为μ=0.25,其余各段均光滑,现有一小球从光滑斜面上的A点由静止释放,那么:
如图所示,半径分别为R=1m,r=0.5m的甲、乙两圆形轨道放置在同一竖直面内,斜面与水平轨道由一小段圆弧轨道相连,两圆形轨道之间由一个水平轨道CD相连,小球与CD段间的动摩擦因数为μ=0.25,其余各段均光滑,现有一小球从光滑斜面上的A点由静止释放,那么:(1)为了是小球能通过甲轨道的最高点,A点离水平轨道CD的高度H至少为多少?
(2)若小球以第(1)问中所求的最小高度由静止从A点滑下,要是小球能到达乙轨道的最高点而做完整的圆周运动,CD段的长度应满足什么条件?
分析 (1)先由圆周运动知识求得D最高点的速度,小球从A运动甲圆形轨道过程中只有重力做功,机械能守恒,根据机械能守恒定律求出小球经过甲圆形轨道的最高点时的位置.
(2)要满足到达乙的最高点的速度不小于$\sqrt{gr}$,由动能定理求距离.
解答 解:(1)刚好通过甲的最高点的速度要求:$mg=m\frac{{v}^{2}}{R}$ ①
由A到甲的最高点由机械能守恒:$mg(H-2R)=\frac{1}{2}m{v}^{2}$ ②
由以上两式可得:H=$\frac{5R}{2}$=2.5m
(2)设CD的长度为x,小球在乙轨道最高点的最小速度为${v}_{2}=\sqrt{gr}$
小球刚好通过乙轨道最高点,根据动能定理得:$mg(\frac{5R}{2}-2r)-μmgx$=$\frac{1}{2}m{v}_{2}^{2}$
得:x=$\frac{5(R-r)}{2μ}$=5m;
答:(1)为了是小球能通过甲轨道的最高点,A点离水平轨道CD的高度H至少为2.5m;
(2)CD段的长度为5m.
点评 本题综合运用了动能定理和圆周运动向心力问题,运用两规律解题时要合适地选择研究的过程进行分析求解.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
15.下列说法正确的是 ( )
| A. | 分子间的距离增大时,分子势能一定增大 | |
| B. | 晶体有确定的熔点,非晶体没有确定的熔点 | |
| C. | 热量总是白发地从分子平均动能大的物体传递到分子平均动能小的物体 | |
| D. | 物体吸热时,它的内能一定增加 | |
| E. | 一定质量的理想气体,如果压强不变,体积增大,那么它一定从外界吸热 |
16.匀强电场中,在沿电场线方向相距25cm的两点间移动4.0×10-5C的电荷时,若要用0.32N的力,则这两点间的电势差为( )
| A. | 3200V | B. | 2000V | C. | 5.12×10-6V | D. | 5.12×106V |
10.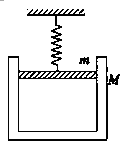 如图所示,活塞的质量为m.缸套的质量为M,通过弹簧吊在天花板上,气缸内封住一定质量的空气,缸套与活塞无摩擦,活塞截面积为S,则下列说法正确的是(P0为大气压强)( )
如图所示,活塞的质量为m.缸套的质量为M,通过弹簧吊在天花板上,气缸内封住一定质量的空气,缸套与活塞无摩擦,活塞截面积为S,则下列说法正确的是(P0为大气压强)( )
 如图所示,活塞的质量为m.缸套的质量为M,通过弹簧吊在天花板上,气缸内封住一定质量的空气,缸套与活塞无摩擦,活塞截面积为S,则下列说法正确的是(P0为大气压强)( )
如图所示,活塞的质量为m.缸套的质量为M,通过弹簧吊在天花板上,气缸内封住一定质量的空气,缸套与活塞无摩擦,活塞截面积为S,则下列说法正确的是(P0为大气压强)( )| A. | 内外空气对缸套的总作用力方向向上,大小为Mg | |
| B. | 内外空气对缸套的总作用力方向向下,大小为mg | |
| C. | 气缸内空气的压强为P0-$\frac{Mg}{S}$ | |
| D. | 气缸内空气的压强为P0+$\frac{mg}{S}$ |
12. 如图,平行板电容器两极板水平放置,现将其和二极管串联接在电源上,已知A和电源正极相连,二极管具有单向导电性.一带电小球沿AB中心水平射入,打在B极板上的N点,小球的重力不能忽略且重力一定大于电场力,现通过上下移动A板来改变两极板AB间距(两极板仍平行),则下列说法正确的是( )
如图,平行板电容器两极板水平放置,现将其和二极管串联接在电源上,已知A和电源正极相连,二极管具有单向导电性.一带电小球沿AB中心水平射入,打在B极板上的N点,小球的重力不能忽略且重力一定大于电场力,现通过上下移动A板来改变两极板AB间距(两极板仍平行),则下列说法正确的是( )
 如图,平行板电容器两极板水平放置,现将其和二极管串联接在电源上,已知A和电源正极相连,二极管具有单向导电性.一带电小球沿AB中心水平射入,打在B极板上的N点,小球的重力不能忽略且重力一定大于电场力,现通过上下移动A板来改变两极板AB间距(两极板仍平行),则下列说法正确的是( )
如图,平行板电容器两极板水平放置,现将其和二极管串联接在电源上,已知A和电源正极相连,二极管具有单向导电性.一带电小球沿AB中心水平射入,打在B极板上的N点,小球的重力不能忽略且重力一定大于电场力,现通过上下移动A板来改变两极板AB间距(两极板仍平行),则下列说法正确的是( )| A. | 若小球带正电,当AB间距增大时,小球将打在N的右侧 | |
| B. | 若小球带正电,当AB间距减小时,小球将打在N的左侧 | |
| C. | 若小球带负电,当AB间距减小时,小球将打在N的右侧 | |
| D. | 若小球带负电,当AB间距增大时,小球将打在N的左侧 |
 木块B放在水平地面上,木块B的质量为0.2kg,在木板上放一质量为1.3kg的A物体A与木板B间、木板与地面间的摩擦因数均为0.4,用水平拉力F将木板B匀速拉出,绳与水平方向成37°.问绳的拉力T多大?水平拉力多大?(tan37°=0.6,cos37°=0.8,g=10m/s2)
木块B放在水平地面上,木块B的质量为0.2kg,在木板上放一质量为1.3kg的A物体A与木板B间、木板与地面间的摩擦因数均为0.4,用水平拉力F将木板B匀速拉出,绳与水平方向成37°.问绳的拉力T多大?水平拉力多大?(tan37°=0.6,cos37°=0.8,g=10m/s2) 如图所示,A、B、C、D为匀强电场中相邻的四个等势面,并且AB=BC=CD,有一个电子垂直经过等势面D时动能为15eV,电子飞经等势面C时电势能为零,飞至等势面A时速度恰好为零,求:
如图所示,A、B、C、D为匀强电场中相邻的四个等势面,并且AB=BC=CD,有一个电子垂直经过等势面D时动能为15eV,电子飞经等势面C时电势能为零,飞至等势面A时速度恰好为零,求: 如图所示,AB为一光滑圆弧,其竖直高度差h1=9.8m,竖直台阶BC高度差为h2,一质量为80kg的物体,从A点由静止滑下,通过B点后水平飞出落到地面CD上,且落地点D到C点的水平距离x=14m,不计空气阻力,g取10m/s2.求:
如图所示,AB为一光滑圆弧,其竖直高度差h1=9.8m,竖直台阶BC高度差为h2,一质量为80kg的物体,从A点由静止滑下,通过B点后水平飞出落到地面CD上,且落地点D到C点的水平距离x=14m,不计空气阻力,g取10m/s2.求: