题目内容
17. 如图所示,AB为一光滑圆弧,其竖直高度差h1=9.8m,竖直台阶BC高度差为h2,一质量为80kg的物体,从A点由静止滑下,通过B点后水平飞出落到地面CD上,且落地点D到C点的水平距离x=14m,不计空气阻力,g取10m/s2.求:
如图所示,AB为一光滑圆弧,其竖直高度差h1=9.8m,竖直台阶BC高度差为h2,一质量为80kg的物体,从A点由静止滑下,通过B点后水平飞出落到地面CD上,且落地点D到C点的水平距离x=14m,不计空气阻力,g取10m/s2.求:(1)物体到达B点的速度vB的大小;
(2)竖直台阶BC高度差h2的大小.
分析 (1)小球由A→B过程中,只有重力做功,根据机械能守恒定律求解v;
(2)小球从B点抛出后做平抛运动,根据平抛运动的位移公式求解h2.
解答 解:(1)根据动能定理可知:$\frac{1}{2}$mvB2=mgh1,
则 vB=$\sqrt{2g{h}_{1}}$=$\sqrt{2×10×9.8}$=14m/s
(2)小球离开B点后做平抛运动,设下落时间为t,则
竖直方向上小球做自由落体运动,有h2=$\frac{1}{2}$gt2 ①
水平方向上小球做匀速直线运动,则物体落地点C到B点的水平距离x=vBt②
①②联立解得h2=5m
答:(1)物体到达B点的速度vB的大小为14m/s;
(2)竖直台阶BC高度差h2的大小为5m.
点评 此题考查动能定理和平抛运动规律,此题也可以应用机械能守恒定律解B点速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.如图是某质点的v-t图象,则( )
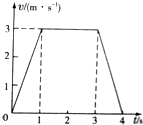

| A. | 在1s到3s时间内质点静止 | |
| B. | 前1s质点做加速运动,最后1s质点做减速运动 | |
| C. | 前1s和最后1s质点的加速度大小均为3m/s2 | |
| D. | 第4s内质点的加速度为0 |
2.有一个铜环和一个木环,它们的形状、尺寸相同.用两块同样的条形磁铁以同样的速度,将N极垂直圆环平面分别插入铜环和木环中,则同一时刻这两环的磁通是( )
| A. | 铜环磁通大 | B. | 木环磁通大 | ||
| C. | 两环磁通一样大 | D. | 两环磁通无法比较 |
6.重离子肿瘤治疗装置中的回旋加速器可发射+5价重离子束,其束流强度为1.2×10-5A,则在1s内发射的重离子个数为(e=1.6×10-19C)( )
| A. | 3.0×1012 | B. | 1.5×1013 | C. | 7.5×1013 | D. | 3.75×1014 |
4. 如图所示为质点做匀变速曲线运动轨迹的示意图,已知质点运动到D点时速度方向与加速度方向恰好互相垂直,则质点从A点运动到E点的过程中,下列说法中正确的是( )
如图所示为质点做匀变速曲线运动轨迹的示意图,已知质点运动到D点时速度方向与加速度方向恰好互相垂直,则质点从A点运动到E点的过程中,下列说法中正确的是( )
 如图所示为质点做匀变速曲线运动轨迹的示意图,已知质点运动到D点时速度方向与加速度方向恰好互相垂直,则质点从A点运动到E点的过程中,下列说法中正确的是( )
如图所示为质点做匀变速曲线运动轨迹的示意图,已知质点运动到D点时速度方向与加速度方向恰好互相垂直,则质点从A点运动到E点的过程中,下列说法中正确的是( )| A. | 质点经过C点的速率比D点的速率大 | |
| B. | 质点经过A点时的加速度方向与速度方向的夹角大于90° | |
| C. | 质点经过D点时的加速度比B点的加速度大 | |
| D. | 质点从B运动到E的过程中加速度方向与速度方向的夹角先增大后减 |


 电子的电荷量的绝对值为e,质量为m,以速度v0沿电场线的方向射入场强为E的匀强电场中,如图所示,电子从A点射入,到B点的速度变为零.
电子的电荷量的绝对值为e,质量为m,以速度v0沿电场线的方向射入场强为E的匀强电场中,如图所示,电子从A点射入,到B点的速度变为零. 如图所示,半径分别为R=1m,r=0.5m的甲、乙两圆形轨道放置在同一竖直面内,斜面与水平轨道由一小段圆弧轨道相连,两圆形轨道之间由一个水平轨道CD相连,小球与CD段间的动摩擦因数为μ=0.25,其余各段均光滑,现有一小球从光滑斜面上的A点由静止释放,那么:
如图所示,半径分别为R=1m,r=0.5m的甲、乙两圆形轨道放置在同一竖直面内,斜面与水平轨道由一小段圆弧轨道相连,两圆形轨道之间由一个水平轨道CD相连,小球与CD段间的动摩擦因数为μ=0.25,其余各段均光滑,现有一小球从光滑斜面上的A点由静止释放,那么: