题目内容
2. 用细线把小球悬挂在墙壁上的钉子O上,小球绕悬点O在竖直平面内做圆周运动.小球质量为m,绳长为L,悬点距地面高度为H.小球运动至最低点时,绳恰被拉断,小球着地时水平位移为S,求:
用细线把小球悬挂在墙壁上的钉子O上,小球绕悬点O在竖直平面内做圆周运动.小球质量为m,绳长为L,悬点距地面高度为H.小球运动至最低点时,绳恰被拉断,小球着地时水平位移为S,求:(1)细线刚被拉断时,小球抛出的速度多大?
(2)细线所能承受的最大拉力?
分析 (1)根据高度求出平抛运动的时间,结合水平位移和时间求出小球抛出时的初速度.
(2)根据牛顿第二定律求出细线所能承受的最大拉力.
解答 解:(1).绳拉断后小球做平抛运动:
水平方向:s=vt,
竖直方向:H-L=$\frac{1}{2}g{t}^{2}$,
解得v=$s\sqrt{\frac{g}{2(H-L)}}$.
(2).小球在最低点,绳子断前:由牛顿第二定律得:
F向=Tm-mg=$m\frac{{v}^{2}}{L}$,
Tm=mg+$\frac{mg{s}^{2}}{2L(H-L)}$.
答:(1)细线刚被拉断时,小球抛出的速度为$s\sqrt{\frac{g}{2(H-L)}}$;
(2)细线所能承受的最大拉力为mg+$\frac{mg{s}^{2}}{2L(H-L)}$.
点评 本题考查了平抛运动和圆周运动的综合运用,知道平抛运动在水平方向和竖直方向上的运动规律,以及圆周运动向心力的来源是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.物体做直线运动,仅受力F的作用,且力F和速度同方向,在力F逐渐减小的过程中物体的运动情况是( )
| A. | 速度减小 | B. | 速度增大 | C. | 加速度变大 | D. | 加速度减小 |
17. 如图所示,x轴在水平地面上,y轴沿竖直方向.图中画出了从y轴上不同位置沿x轴正向水平抛出的三个小球a、b和c的运动轨迹.小球a从(0,2L)抛出,落在(2L,0)处;小球b、c从(0,L)抛出,分别落在(2L,0)和(L,0)处.不计空气阻力,下列说法正确的是( )
如图所示,x轴在水平地面上,y轴沿竖直方向.图中画出了从y轴上不同位置沿x轴正向水平抛出的三个小球a、b和c的运动轨迹.小球a从(0,2L)抛出,落在(2L,0)处;小球b、c从(0,L)抛出,分别落在(2L,0)和(L,0)处.不计空气阻力,下列说法正确的是( )
 如图所示,x轴在水平地面上,y轴沿竖直方向.图中画出了从y轴上不同位置沿x轴正向水平抛出的三个小球a、b和c的运动轨迹.小球a从(0,2L)抛出,落在(2L,0)处;小球b、c从(0,L)抛出,分别落在(2L,0)和(L,0)处.不计空气阻力,下列说法正确的是( )
如图所示,x轴在水平地面上,y轴沿竖直方向.图中画出了从y轴上不同位置沿x轴正向水平抛出的三个小球a、b和c的运动轨迹.小球a从(0,2L)抛出,落在(2L,0)处;小球b、c从(0,L)抛出,分别落在(2L,0)和(L,0)处.不计空气阻力,下列说法正确的是( )| A. | b和c运动时间相同 | B. | a和b初速度相同 | ||
| C. | a的运动时间是b的两倍 | D. | b的初速度是c的两倍 |
7. 如图所示,A、B都是较轻的铝环,A环闭合,B环断开,横梁可以绕中间支点自由转动,开始时整个装置静止.下列说法中正确的是( )
如图所示,A、B都是较轻的铝环,A环闭合,B环断开,横梁可以绕中间支点自由转动,开始时整个装置静止.下列说法中正确的是( )
 如图所示,A、B都是较轻的铝环,A环闭合,B环断开,横梁可以绕中间支点自由转动,开始时整个装置静止.下列说法中正确的是( )
如图所示,A、B都是较轻的铝环,A环闭合,B环断开,横梁可以绕中间支点自由转动,开始时整个装置静止.下列说法中正确的是( )| A. | 条形磁铁插入A环时,横梁不会发生转动 | |
| B. | 只有当条形磁铁N极拔出铝环时,横梁才会转动 | |
| C. | 条形磁铁用相同方式分别插入A、B环时,两环转动情况相同 | |
| D. | 铝环A产生的感应电流总是阻碍铝环与磁铁间的相对运动 |
14.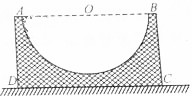 某大型游乐场内的新型滑行运动可以等效为如图所示的物理模型.大型矩形台内有半圆柱形凹槽.一个小朋友在A点由静止开始滑人凹槽内.不计滑板与圆形凹槽间的摩擦,滑到另一端B处恰好静止,整个过程中矩形台保持静止状态.则该小朋友从A点滑至B端的过程中( )
某大型游乐场内的新型滑行运动可以等效为如图所示的物理模型.大型矩形台内有半圆柱形凹槽.一个小朋友在A点由静止开始滑人凹槽内.不计滑板与圆形凹槽间的摩擦,滑到另一端B处恰好静止,整个过程中矩形台保持静止状态.则该小朋友从A点滑至B端的过程中( )
 某大型游乐场内的新型滑行运动可以等效为如图所示的物理模型.大型矩形台内有半圆柱形凹槽.一个小朋友在A点由静止开始滑人凹槽内.不计滑板与圆形凹槽间的摩擦,滑到另一端B处恰好静止,整个过程中矩形台保持静止状态.则该小朋友从A点滑至B端的过程中( )
某大型游乐场内的新型滑行运动可以等效为如图所示的物理模型.大型矩形台内有半圆柱形凹槽.一个小朋友在A点由静止开始滑人凹槽内.不计滑板与圆形凹槽间的摩擦,滑到另一端B处恰好静止,整个过程中矩形台保持静止状态.则该小朋友从A点滑至B端的过程中( )| A. | 地面对矩形台的摩擦力方向先水平向左,后水平向右 | |
| B. | 地面对矩形台的摩擦力方向先水平向右,后水平向左 | |
| C. | 地面对矩形台的支持力的大小始终大于小朋友,滑板和滑梯的总重力的大小 | |
| D. | 地面对矩形台的支持力的大小先小于、后大于、再小于小朋友、滑板和矩形台总重力的大小 |
11. 如图所示,匀强电场竖直向上,匀强磁场的方向垂直纸面向外.有一正离子(不计重力),恰能沿直线从左向右水平飞越此区域.则( )
如图所示,匀强电场竖直向上,匀强磁场的方向垂直纸面向外.有一正离子(不计重力),恰能沿直线从左向右水平飞越此区域.则( )
 如图所示,匀强电场竖直向上,匀强磁场的方向垂直纸面向外.有一正离子(不计重力),恰能沿直线从左向右水平飞越此区域.则( )
如图所示,匀强电场竖直向上,匀强磁场的方向垂直纸面向外.有一正离子(不计重力),恰能沿直线从左向右水平飞越此区域.则( )| A. | 若电子从右向左水平飞入,电子也沿直线运动 | |
| B. | 若电子从右向左水平飞入,电子将向上偏 | |
| C. | 若电子从右向左水平飞入,电子将向下偏 | |
| D. | 若电子从右向左水平飞入,则无法判断电子是否偏转 |
18.两端封闭的竖直放置的玻璃管的中部有一段水银,水银柱的上、下方存有密闭气体,当它在竖直方向运动时,发现水银柱相对玻璃在向上移动,则下列说法中正确的是( )
| A. | 玻璃管做匀速运动,环境温度升高 | B. | 温度不变,玻璃管向下做加速运动 | ||
| C. | 温度不变,玻璃管向下做减速运动 | D. | 温度降低,玻璃管向下做减速运动 |
 在“用单摆测定重力加速度”的实验中:
在“用单摆测定重力加速度”的实验中: 如图所示,士兵射击训练时,射击枪水平放置,射击枪与目标靶中心位于离地面足够高的同一水平线上,枪口与目标靶之间的距离s=100m,子弹射出的水平速度v=250m/s,子弹从枪口射出的瞬 间目标靶由静止开始释放,不计空气阻力,取重力加速度g为10m/s2,求:
如图所示,士兵射击训练时,射击枪水平放置,射击枪与目标靶中心位于离地面足够高的同一水平线上,枪口与目标靶之间的距离s=100m,子弹射出的水平速度v=250m/s,子弹从枪口射出的瞬 间目标靶由静止开始释放,不计空气阻力,取重力加速度g为10m/s2,求: