��Ŀ����
9��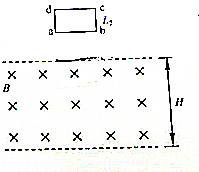 ��ͼ�����ε��ѵ��߿�abcd������Ϊm������ΪR����ab�߳�L1��bc�߳�L2����ʼʱ�߿�ֹ����ֱƽ������ab��ˮƽ���߿��·�һ�����봦��һ���������ڴ��ڷ���ֱ���߿�ƽ�桢�Ÿ�Ӧǿ�ȴ�СΪB����ǿ�ų��ϡ��±߽�����߿�ab��ƽ�У��ų������ڵĸ߶ȴ���L2�����ֽ��߿��ɾ�ֹ���ͷţ����߿����������ab����ų��߽�ʼ��ƽ���ҷ���ˮƽ����֪ab�߸ս���ų��մ����ų�ʱ���߿�������ֱ���˶������ٶȴ�С��Ϊ$\frac{g}{4}$����cd�߳��ų�ǰ˲�䣬�߿���ٶ�ǡ��Ϊ�㣬���ƿ����������������ٶ�Ϊg����
��ͼ�����ε��ѵ��߿�abcd������Ϊm������ΪR����ab�߳�L1��bc�߳�L2����ʼʱ�߿�ֹ����ֱƽ������ab��ˮƽ���߿��·�һ�����봦��һ���������ڴ��ڷ���ֱ���߿�ƽ�桢�Ÿ�Ӧǿ�ȴ�СΪB����ǿ�ų��ϡ��±߽�����߿�ab��ƽ�У��ų������ڵĸ߶ȴ���L2�����ֽ��߿��ɾ�ֹ���ͷţ����߿����������ab����ų��߽�ʼ��ƽ���ҷ���ˮƽ����֪ab�߸ս���ų��մ����ų�ʱ���߿�������ֱ���˶������ٶȴ�С��Ϊ$\frac{g}{4}$����cd�߳��ų�ǰ˲�䣬�߿���ٶ�ǡ��Ϊ�㣬���ƿ����������������ٶ�Ϊg������1�����߿����ų������У�ͨ���߿���ijһ����ĵ���q��
��2����cd�߸ս���ų�ʱ���߿��ٶȴ�Сv��
��3���߿�Խ�ų���������У��߿�������������Q��
��4���ų�����ĸ߶�H��
��5���߿�ӿ�ʼ���䵽�뿪�ų�������������ʱ��t��
���� ��1�����ݷ����ڵ�Ÿ�Ӧ���ɡ�ŷķ���ɺ͵����Ķ���ʽ������q��
��2�������߿����ʹ����ų����̵�������֪����cd�߽��ų�˲����ٶ�Ϊ�㣬�ɰ��������ٶȵĹ�ϵ��ƽ���������߿���ٶȴ�Сv��
��3������ţ�ٵڶ����ɺͰ��������ٶȵĹ�ϵʽ������߿�ս���ų�ʱ���ٶȣ����������غ㶨��������Q��
��4���߿���ȫ�ڴų����˶�ʱ��������Ӧ���������ܰ����������ػ�е���غ㣬�ɻ�е���غ㶨����H��
��5���о��߿����ų��Ĺ��̣���ţ�ٵڶ����ɺͼ��ٶȵĶ���ʽ�����û��ַ���ʱ�䣮���ȱ���ֱ���˶���λ��ʱ�乫ʽ����߿��cd�߸մų���ab�߸ճ��ų���ʱ�䣮�Ӷ��������ʱ�䣮
��� �⣺��1�����߿����ų������У�ͨ���߿���ijһ����ĵ��� q=$\overline{I}t$=$\frac{\overline{E}}{R}t$=$\frac{B{L}_{1}\overline{v}t}{R}$=$\frac{B{L}_{1}{L}_{2}}{R}$
��2�������߿����ʹ����ų����̵�������֪����cd�߽��ų�˲����ٶ�Ϊ�㣬����
mg=F����
�ְ����� F��=BIL1=B$\frac{B{L}_{1}v}{R}$L1=$\frac{{B}^{2}{L}_{1}^{2}v}{R}$
������� v=$\frac{mgR}{{B}^{2}{L}_{1}^{2}}$
��3�����߿�ս���ų�ʱ���ٶ�Ϊv0��
����ţ�ٵڶ����ɵã�$\frac{{B}^{2}{L}_{1}^{2}{v}_{0}}{R}$-mg=ma=m$•\frac{g}{4}$
��� v0=$\frac{5mgR}{4{B}^{2}{L}_{1}^{2}}$
�߿�Խ�ų���������У����������غ㶨�ɵ�
Q=2��[��$\frac{1}{2}m{v}_{0}^{2}-\frac{1}{2}m{v}^{2}$��+mgL1]=$\frac{9{m}^{3}{g}^{2}{R}^{2}}{32{B}^{4}{L}_{1}^{4}}$+2mgL1
��4�������߿���ȫ�ڴų����˶��Ĺ��̣����˶�ѧ��ʽ��
v02-v2=2g��H-2L2��
��� H=$\frac{9{m}^{2}g{R}^{2}}{32{B}^{4}{L}_{1}^{4}}$+2L2��
��5���߿����������ʱ�� t1=$\frac{{v}_{0}}{g}$=$\frac{5mR}{4{B}^{2}{L}_{1}^{2}}$
�о��߿����ų��Ĺ��̣���ţ�ٵڶ����ɵ�
$\frac{{B}^{2}{L}_{1}^{2}{v}_{0}}{R}$-mg=ma=m$\frac{��v}{��t}$
�� $\frac{{B}^{2}{L}_{1}^{2}{v}_{0}}{R}$��t-mg��t=m��v
������͵ã�$\sum_{\;}^{\;}$��$\frac{{B}^{2}{L}_{1}^{2}{v}_{0}}{R}$��t��-$\sum_{\;}^{\;}$��mg��t��=$\sum_{\;}^{\;}$m��v
�ɵ� $\frac{{B}^{2}{L}_{1}^{2}}{R}$•L2-mgt2=m��v0-v��
����߿����ų���ʱ�� t2=$\frac{{B}^{2}{L}_{1}^{2}{L}_{2}}{mgR}$-$\frac{mR}{{B}^{2}{L}_{1}^{2}}$
�߿��cd�߸մų���ab�߸ճ��ų���ʱ����Ϊt3��
�� t3=$\frac{{v}_{0}-v}{g}$=$\frac{mR}{4{B}^{2}{L}_{1}^{2}}$
���߿�ӿ�ʼ���䵽�뿪�ų�������������ʱ�� t=t1+2t2+t3=$\frac{2{B}^{2}{L}_{1}^{2}{L}_{2}}{mgR}$-$\frac{mR}{2{B}^{2}{L}_{1}^{2}}$��
��
��1�����߿����ų������У�ͨ���߿���ijһ����ĵ���q��$\frac{B{L}_{1}{L}_{2}}{R}$��
��2����cd�߸ս���ų�ʱ���߿��ٶȴ�Сv��$\frac{mgR}{{B}^{2}{L}_{1}^{2}}$��
��3���߿�Խ�ų���������У��߿�������������Q��$\frac{9{m}^{3}{g}^{2}{R}^{2}}{32{B}^{4}{L}_{1}^{4}}$+2mgL1��
��4���ų�����ĸ߶�H��$\frac{9{m}^{2}g{R}^{2}}{32{B}^{4}{L}_{1}^{4}}$+2L2��
��5���߿�ӿ�ʼ���䵽�뿪�ų�������������ʱ��t��$\frac{2{B}^{2}{L}_{1}^{2}{L}_{2}}{mgR}$-$\frac{mR}{2{B}^{2}{L}_{1}^{2}}$��
���� ����Ҫ��������߿���˶����̣������Ƶ��������Ͱ������ı���ʽ������ţ�ٵڶ����ɺͼ��ٶȵĶ���ʽ���߿����ų���ʱ���ǹؼ���

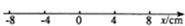 ��ͼ��ʾ��һ�ʵ���x������OΪƽ��λ������г�˶��������Ϊ8cm������Ϊ4s��t=0ʱ������x=4cm������x�Ḻ�����˶���������
��ͼ��ʾ��һ�ʵ���x������OΪƽ��λ������г�˶��������Ϊ8cm������Ϊ4s��t=0ʱ������x=4cm������x�Ḻ�����˶���������| A�� | �ʵ���t=1��Osʱ������λ��Ϊx=+4$\sqrt{3}$cm | |
| B�� | �ʵ���t=1��Osʱ������λ��Ϊx=-4$\sqrt{3}$cm | |
| C�� | ����ʼλ���˶���x=-4cm����������ʱ��Ϊ$\frac{2}{3}$s | |
| D�� | ����ʼλ�D�˶���x=-4cm����������ʱ��Ϊ$\frac{1}{6}$s |
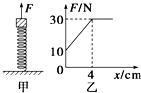 ��ͼa��ʾ��һ���ʵ��ɵ��¶˹̶���ˮƽ���ϣ��϶˷���һ���壨�����뵯�ɲ����ӣ�����ʼʱ���崦�ھ�ֹ״̬��������ֱ���ϵ�����F�����������ϣ�ʹ���忪ʼ�������ȼ����˶�������F������λ��x֮��Ĺ�ϵ��ͼb��ʾ��g=10m/s2���������н�����ȷ���ǣ�������
��ͼa��ʾ��һ���ʵ��ɵ��¶˹̶���ˮƽ���ϣ��϶˷���һ���壨�����뵯�ɲ����ӣ�����ʼʱ���崦�ھ�ֹ״̬��������ֱ���ϵ�����F�����������ϣ�ʹ���忪ʼ�������ȼ����˶�������F������λ��x֮��Ĺ�ϵ��ͼb��ʾ��g=10m/s2���������н�����ȷ���ǣ�������| A�� | ���������Ϊ3kg | B�� | ����ļ��ٶȴ�СΪ5m/s2 | ||
| C�� | ���ɵľ���ϵ��Ϊ7.5N/cm | D�� | �����뵯�ɷ���ʱ����Ϊ0.4J |
 �ų���ǿ�����ż������Ĵų��ܱ�����λ�õĴų�ǿ���ų�ǿ��������ͬ�Ĵų�������ǿ�ų����ų�ǿ�ȵĵ�λ����˹��������أ�����T��ͨ�絼���ڴų����ܵ��������ã�������������������������Ĵ�С������ų�ǿ�ȴ�С�йأ����������С�йأ�ʵ���������ǿ�ų��У���ͨ�絼����ų�����ֱʱ���������ܵİ�����F���ڴų�ǿ��B������I�͵��߳���L���ߵij˻�����F=BIL��
�ų���ǿ�����ż������Ĵų��ܱ�����λ�õĴų�ǿ���ų�ǿ��������ͬ�Ĵų�������ǿ�ų����ų�ǿ�ȵĵ�λ����˹��������أ�����T��ͨ�絼���ڴų����ܵ��������ã�������������������������Ĵ�С������ų�ǿ�ȴ�С�йأ����������С�йأ�ʵ���������ǿ�ų��У���ͨ�絼����ų�����ֱʱ���������ܵİ�����F���ڴų�ǿ��B������I�͵��߳���L���ߵij˻�����F=BIL��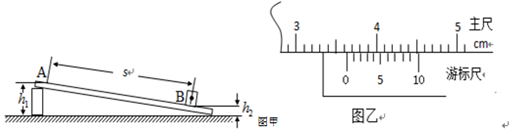
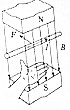
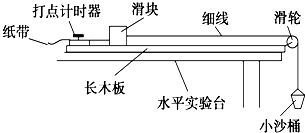 ij̽��ѧϰС���ͬѧ����֤�����ܶ�������������ʵ������װ��һ����ͼ��ʾ��װ�ã�������С���е�һλ��Ա��Ҫ��ɸ���ʵ�飬��
ij̽��ѧϰС���ͬѧ����֤�����ܶ�������������ʵ������װ��һ����ͼ��ʾ��װ�ã�������С���е�һλ��Ա��Ҫ��ɸ���ʵ�飬��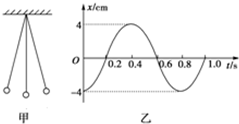 ͼ����һ�����������Σ�ͼ����������ڵ���ͼ�������ص��������ٶ�Ϊg=��2 m/s2��������ڵİڳ�Ϊ0.16�ף�
ͼ����һ�����������Σ�ͼ����������ڵ���ͼ�������ص��������ٶ�Ϊg=��2 m/s2��������ڵİڳ�Ϊ0.16�ף� һ�֡�ɵ�ϡ�������ع�ʱ���ǹ̶�����ģ�Ϊ�˹���������ع�ʱ�䣬��λͬѧ���������ʵ�鷽��������ǽ��ǰij�㣬ʹһ��Сʯ���������£���Сʯ�����࣬�õ���ͼ����Ƭ������Сʯ�ӵ��˶���������Ƭ������һ��ģ���ľ���AB����֪ÿ��ש��ƽ�����ԼΪ6cm����������㵽A�������ֱ����Լ1.8m������Щ��Ϣ�����������ع�ʱ����ӽ��ڣ�������
һ�֡�ɵ�ϡ�������ع�ʱ���ǹ̶�����ģ�Ϊ�˹���������ع�ʱ�䣬��λͬѧ���������ʵ�鷽��������ǽ��ǰij�㣬ʹһ��Сʯ���������£���Сʯ�����࣬�õ���ͼ����Ƭ������Сʯ�ӵ��˶���������Ƭ������һ��ģ���ľ���AB����֪ÿ��ש��ƽ�����ԼΪ6cm����������㵽A�������ֱ����Լ1.8m������Щ��Ϣ�����������ع�ʱ����ӽ��ڣ�������