题目内容
20.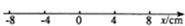 如图所示,一质点在x轴上以O为平衡位置做简谐运动,其振幅为8cm,周期为4s.t=0时物体在x=4cm处,向x轴负方向运动,则( )
如图所示,一质点在x轴上以O为平衡位置做简谐运动,其振幅为8cm,周期为4s.t=0时物体在x=4cm处,向x轴负方向运动,则( )| A. | 质点在t=1.Os时所处的位置为x=+4$\sqrt{3}$cm | |
| B. | 质点在t=1.Os时所处的位置为x=-4$\sqrt{3}$cm | |
| C. | 由起始位置运动到x=-4cm处所需的最短时间为$\frac{2}{3}$s | |
| D. | 由起始位罝运动到x=-4cm处所需的最短时间为$\frac{1}{6}$s |
分析 简谐运动振动方程的一般表达式x=Asin(ωt+φ0),由ω=$\frac{2π}{T}$求出ω.将在t=0时,位移是4cm代入即可求解振动方程.然后依据该方程分析即可.
解答 解:简谐运动振动方程的一般表示式为:x=Asin(ωt+φ0),
根据题给条件有:A=8cm=0.08m,ω=$\frac{2π}{T}=\frac{2π}{4}=0.5π$ rad/s
所以 x=0.08sin(0.5πt+φ0)m
将t=0时,x0=0.04m
代入得:0.04=0.08sinφ0
解得初相:φ0=$\frac{π}{6}$或φ0=$\frac{5π}{6}$
因为t=0时,速度方向沿x轴负方向,即位移在减小,所以取 φ0=$\frac{5π}{6}$
所求的振动方程为:x=0.08sin(0.5πt+$\frac{5π}{6}$)m
A、质点在t=1.Os时所处的位置为x=0.08sin(0.5π×1+$\frac{5π}{6}$)=-0.04$\sqrt{3}$m=-4$\sqrt{3}$cm.故A错误,B正确;
C、由于t=0时刻质点向x轴负方向运动,所以由起始位置运动到x=-4cm处所需的最短时间为回到平衡位置后直接再到达x=-4cm处的时间,由振动的对称性可知,两段时间相等.回到平衡位置的时间:${t}_{1}=\frac{π-\frac{5π}{6}}{ω}=\frac{\frac{π}{6}}{0.5π}=\frac{1}{3}$s,所以由起始位置运动到x=-4cm处所需的最短时间为t=2t1=$\frac{2}{3}$s.故C正确,D错误.
故选:BC
点评 本题关键记住简谐运动的一般表达式x=Asin(ωt+φ0),掌握ω=2πf=$\frac{2π}{T}$,然后采用代入法求解.

 阅读快车系列答案
阅读快车系列答案| A. | 它就是液体分子的运动 | B. | 它反映了液体分子的运动 | ||
| C. | 它的激烈程度跟液体温度有关 | D. | 它的运动是毫无规则的 |
 如图甲所示,将质量为M的物块A和质量为m的物块B放在水平转盘上,两者用长为L的水平轻绳连接,物块与转盘的最大静摩擦力均为各自重力的k倍,物块A与转轴的距离等于轻绳长度,整个装置能绕过转盘中心的竖直轴转动,开始时,轻绳恰好伸直但无弹力,现让该装置从静止开始转动,使角速度缓慢增大,绳中张力FT与转动角速度的平方ω2的关系如图乙所示,当角速度的平方ω2超过3ω${\;}_{1}^{2}$时,物块A,B开始滑行,若图乙中的F1,ω1及重力加速度g均为已知,下列说法正确的是( )
如图甲所示,将质量为M的物块A和质量为m的物块B放在水平转盘上,两者用长为L的水平轻绳连接,物块与转盘的最大静摩擦力均为各自重力的k倍,物块A与转轴的距离等于轻绳长度,整个装置能绕过转盘中心的竖直轴转动,开始时,轻绳恰好伸直但无弹力,现让该装置从静止开始转动,使角速度缓慢增大,绳中张力FT与转动角速度的平方ω2的关系如图乙所示,当角速度的平方ω2超过3ω${\;}_{1}^{2}$时,物块A,B开始滑行,若图乙中的F1,ω1及重力加速度g均为已知,下列说法正确的是( )| A. | L=$\frac{{F}_{1}}{m{ω}_{1}^{2}}$ | B. | L=$\frac{{F}_{1}}{2m{ω}_{1}^{2}}$ | C. | k=$\frac{2{F}_{1}}{mg}$ | D. | m=M |
| A. | 布朗运动是指液体或气体中悬浮微粒的无规则运动 | |
| B. | 气体的温度升高,每个气体分子运动的速率都增加 | |
| C. | 液晶显示器利用了液晶对光具有各向异性的特点 | |
| D. | 对某物体做功,必定会使该物体的内能增加 | |
| E. | 功转变为热的实际宏观过程是不可逆过程 |
 节日里悬挂灯笼是我国的一种民俗.由于建筑物位置原因,悬挂时A、B点高度不同,O为结点,轻绳AO、BO长度相等,拉力分别为FA、FB,灯笼受到的重力为G.下列表述正确的是( )
节日里悬挂灯笼是我国的一种民俗.由于建筑物位置原因,悬挂时A、B点高度不同,O为结点,轻绳AO、BO长度相等,拉力分别为FA、FB,灯笼受到的重力为G.下列表述正确的是( )| A. | FA一定小于G | B. | FA一定小于FB | ||
| C. | FA与FB大小相等 | D. | FA与FB大小之和等于G |
| A. | 与行星距太阳间的距离成正比 | B. | 与行星距太阳间的距离成反比 | ||
| C. | 与行星运动速率的平方成正比 | D. | 与行星距太阳的距离的平方成反比 |
| A. | 1:4 | B. | 1:2 | C. | 4:1 | D. | 2:1 |
 为“验证牛顿第二定律”,某同学设计了如下实验方案:A.实验装置如图甲所示,一端系在滑块上的轻质细绳通过转轴光滑的轻质滑轮,另一端挂一质量为m=0.5kg的钩码,用垫块将长木板的有定滑轮的一端垫起.调整长木板的倾角,直至轻推滑块后,滑块沿长木板向下做匀速直线运动;B.保持长木板的倾角不变,取下细绳和钩码,接好纸带,接通打点计时器的电源,然后让滑块沿长木板滑下,打点计时器打下的纸带如图乙所示.请回答下列问题:
为“验证牛顿第二定律”,某同学设计了如下实验方案:A.实验装置如图甲所示,一端系在滑块上的轻质细绳通过转轴光滑的轻质滑轮,另一端挂一质量为m=0.5kg的钩码,用垫块将长木板的有定滑轮的一端垫起.调整长木板的倾角,直至轻推滑块后,滑块沿长木板向下做匀速直线运动;B.保持长木板的倾角不变,取下细绳和钩码,接好纸带,接通打点计时器的电源,然后让滑块沿长木板滑下,打点计时器打下的纸带如图乙所示.请回答下列问题: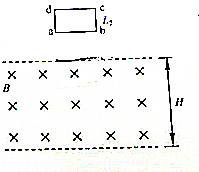 如图,矩形单匝导线框abcd的质量为m,电阻为R,其ab边长L1、bc边长L2,开始时线框静止于竖直平面内且ab边水平,线框下方一定距离处的一矩形区域内存在方向垂直于线框平面、磁感应强度大小为B的匀强磁场上、下边界均与线框ab边平行(磁场区域内的高度大于L2),现将线框由静止起释放,设线框下落过程中ab边与磁场边界始终平行且方向水平,已知ab边刚进入磁场和刚穿出磁场时,线框都作减速直线运动,加速度大小均为$\frac{g}{4}$,而cd边出磁场前瞬间,线框加速度恰好为零,不计空气阻力,重力加速度为g.求:
如图,矩形单匝导线框abcd的质量为m,电阻为R,其ab边长L1、bc边长L2,开始时线框静止于竖直平面内且ab边水平,线框下方一定距离处的一矩形区域内存在方向垂直于线框平面、磁感应强度大小为B的匀强磁场上、下边界均与线框ab边平行(磁场区域内的高度大于L2),现将线框由静止起释放,设线框下落过程中ab边与磁场边界始终平行且方向水平,已知ab边刚进入磁场和刚穿出磁场时,线框都作减速直线运动,加速度大小均为$\frac{g}{4}$,而cd边出磁场前瞬间,线框加速度恰好为零,不计空气阻力,重力加速度为g.求: