题目内容
17.某同学为了测定滑块与木板的动摩擦因数,设计实验装置如图甲;长直平板一端放在水平桌面上,另一端架在一物块上;在平板上标出A、B两点,B点放处置一光电门,用光电计时器记录滑块上的挡光条通过光电门时挡光时间.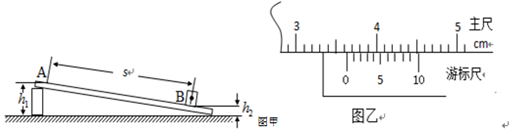
实验步骤如下:
①用游标卡尺测量挡光条的宽度d;
②用直尺测量AB之间的距离s,A点到水平桌面的垂直距离h1,B点到水平桌面的垂直距离h2;
③将滑块从A点由静止释放,由光电计时器读出滑块的挡光时间t;依据测量数据可计算出动摩擦因数μ;
④改变斜面的倾角,重复时间步骤②③,得到多个μ值,求出平均值,写入实验报告.
(1)测量挡光条宽度时的游标卡尺度数如图乙所示,读得d=36.2mm.
(2)对应于题中②③步的测量,完成下列各式.(已知重力加速度为g)
①斜面倾角的余弦cosθ=$\frac{\sqrt{{s}^{2}-{({h}_{1}-{h}_{2})}^{2}}}{s}$;
②滑块运动时的加速度a=$\frac{{d}^{2}}{2s{t}^{2}}$;
③滑块与斜面的动摩擦因数μ=$\frac{{2g({h_1}-{h_2}){t^2}-{d^2}}}{{2g{t^2}\sqrt{{s^2}-{{({h_1}-{h_2})}^2}}}}$(用斜面倾角θ与加速度a表示).
分析 某同学为了测定滑块与木板的动摩擦因数,设计实验装置如图甲;长直平板一端放在水平桌面上,另一端架在一物块上;在平板上标出A、B两点,B点放处置一光电门,用光电计时器记录滑块上的挡光条通过光电门时挡光时间.
解答 解:(1)、游标卡尺的主尺读数为3.6cm=36mm,游标尺上第2个刻度和主尺上某一刻度对齐,因此其读数为为0.1×2mm=0.2mm,所以最终读数为:36mm+0.1mm=3.62mm;
(2)①由数学知识可知:cosα=$\frac{\sqrt{{s}^{2}-{({h}_{1}-{h}_{2})}^{2}}}{s}$;
②、滑块通过光电门时的速度:v=$\frac{d}{t}$;
由v2-v02=2ax可得:v2=2as,即:($\frac{d}{t}$)2=2as,
解得,加速度:a=$\frac{{d}^{2}}{2s{t}^{2}}$;
③、由牛顿第二定律得:mgsinθ-f=ma,
其中sinθ=$\frac{{h}_{1}-{h}_{2}}{s}$,
解得f=mg$\frac{{h}_{1}-{h}_{2}}{s}$-m$\frac{{d}^{2}}{2s{t}^{2}}$;
f=μmgcosθ
联立各式解得μ=$\frac{2g({h}_{1}-{h}_{2}){t}^{2}-{d}^{2}}{2g{t}^{2}\sqrt{{s}^{2}-{({h}_{1}-{h}_{2})}^{2}}}$
故答案为:(1)36.2 (2)①$\frac{\sqrt{{s}^{2}-{({h}_{1}-{h}_{2})}^{2}}}{s}$,②$\frac{{d}^{2}}{2s{t}^{2}}$;③$\frac{{2g({h_1}-{h_2}){t^2}-{d^2}}}{{2g{t^2}\sqrt{{s^2}-{{({h_1}-{h_2})}^2}}}}$
点评 熟练应用数学知识和牛顿第二定律以及运动学公式解决问题;掌握游标卡尺读数的方法,主尺读数加上游标读数,不需估读.
本题难度不大,是一道基础题,认真审题、熟练应用数学知识,并把握匀变速直线运动的特点和本实验的实验原理是解决此题的前提

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案| A. | $\sqrt{\frac{m}{M+m}}$•v1 | B. | $\sqrt{\frac{M+m}{M}}$•v1 | C. | $\sqrt{\frac{M}{M+m}}$•v1 | D. | $\sqrt{\frac{M+m}{m}}$•v1 |
| A. | 布朗运动是指液体或气体中悬浮微粒的无规则运动 | |
| B. | 气体的温度升高,每个气体分子运动的速率都增加 | |
| C. | 液晶显示器利用了液晶对光具有各向异性的特点 | |
| D. | 对某物体做功,必定会使该物体的内能增加 | |
| E. | 功转变为热的实际宏观过程是不可逆过程 |
| A. | 与行星距太阳间的距离成正比 | B. | 与行星距太阳间的距离成反比 | ||
| C. | 与行星运动速率的平方成正比 | D. | 与行星距太阳的距离的平方成反比 |

| A. | 甲摆的振幅比乙摆的振幅大 | |
| B. | 甲摆的机械能比乙摆的机械能大 | |
| C. | 甲、乙两单摆的摆长相等 | |
| D. | 在t=0.5 s时有正向最大加速度的是乙摆 |
 矩形线框在匀强磁场内匀速转动过程中,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )
矩形线框在匀强磁场内匀速转动过程中,线框输出的交流电压随时间变化的图象如图所示,下列说法中正确的是( )| A. | 1 s末线框平面垂直于磁场,通过线框的磁通量变化最快 | |
| B. | 2 s末线框平面垂直于磁场,通过线框的磁通量最大 | |
| C. | 交流电压的最大值为36$\sqrt{2}$V,频率为0.25Hz | |
| D. | 交流电压的最大值为36V,周期为4 s |
 如图所示,是一个做匀变速曲线运动的物块的运动轨迹示意图,运动至A时速度大小为v0,经一段时间后物块运动至B点,速度大小仍为v0,则在此过程中( )
如图所示,是一个做匀变速曲线运动的物块的运动轨迹示意图,运动至A时速度大小为v0,经一段时间后物块运动至B点,速度大小仍为v0,则在此过程中( )| A. | 物块的合外力与A点v0同向 | |
| B. | 物块的合外力与B点v0同向 | |
| C. | 因为A、B两点速度大小相同,故物块加速度为0 | |
| D. | 物块的加速度不变 |
 为“验证牛顿第二定律”,某同学设计了如下实验方案:A.实验装置如图甲所示,一端系在滑块上的轻质细绳通过转轴光滑的轻质滑轮,另一端挂一质量为m=0.5kg的钩码,用垫块将长木板的有定滑轮的一端垫起.调整长木板的倾角,直至轻推滑块后,滑块沿长木板向下做匀速直线运动;B.保持长木板的倾角不变,取下细绳和钩码,接好纸带,接通打点计时器的电源,然后让滑块沿长木板滑下,打点计时器打下的纸带如图乙所示.请回答下列问题:
为“验证牛顿第二定律”,某同学设计了如下实验方案:A.实验装置如图甲所示,一端系在滑块上的轻质细绳通过转轴光滑的轻质滑轮,另一端挂一质量为m=0.5kg的钩码,用垫块将长木板的有定滑轮的一端垫起.调整长木板的倾角,直至轻推滑块后,滑块沿长木板向下做匀速直线运动;B.保持长木板的倾角不变,取下细绳和钩码,接好纸带,接通打点计时器的电源,然后让滑块沿长木板滑下,打点计时器打下的纸带如图乙所示.请回答下列问题: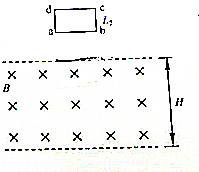 如图,矩形单匝导线框abcd的质量为m,电阻为R,其ab边长L1、bc边长L2,开始时线框静止于竖直平面内且ab边水平,线框下方一定距离处的一矩形区域内存在方向垂直于线框平面、磁感应强度大小为B的匀强磁场上、下边界均与线框ab边平行(磁场区域内的高度大于L2),现将线框由静止起释放,设线框下落过程中ab边与磁场边界始终平行且方向水平,已知ab边刚进入磁场和刚穿出磁场时,线框都作减速直线运动,加速度大小均为$\frac{g}{4}$,而cd边出磁场前瞬间,线框加速度恰好为零,不计空气阻力,重力加速度为g.求:
如图,矩形单匝导线框abcd的质量为m,电阻为R,其ab边长L1、bc边长L2,开始时线框静止于竖直平面内且ab边水平,线框下方一定距离处的一矩形区域内存在方向垂直于线框平面、磁感应强度大小为B的匀强磁场上、下边界均与线框ab边平行(磁场区域内的高度大于L2),现将线框由静止起释放,设线框下落过程中ab边与磁场边界始终平行且方向水平,已知ab边刚进入磁场和刚穿出磁场时,线框都作减速直线运动,加速度大小均为$\frac{g}{4}$,而cd边出磁场前瞬间,线框加速度恰好为零,不计空气阻力,重力加速度为g.求: