题目内容
15.已知万有引力常量G,地球半径R,月球和地球之间的距离r,地球同步卫星距地面的高度h,月球绕地球的运转周期T1,地球的自转周期T2,地球表面的重力加速度g.根据以上条件,正确计算地球质量M的关系式是( )| A. | $M=\frac{{4{π^2}{h^3}}}{{G{T_2}^2}}$ | B. | $M=\frac{{g{R^2}}}{G}$ | ||
| C. | $M=\frac{{4{π^2}{r^3}}}{{G{T_1}^2}}$ | D. | $M=\frac{{4{π^2}{{(R+h)}^3}}}{{G{T_2}^2}}$ |
分析 根据万有引力等于重力和万有引力提供向心力求解中心天体(地球)的质量.
解答 解:AD、地球同步卫星绕地球做匀速圆周运动,万有引力提供向心力,周期等于地球的自转周期${T}_{2}^{\;}$,轨道半径R+h
根据$G\frac{Mm}{(R+h)_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{2}^{2}}(R+h)$,解得地球质量$M=\frac{4{π}_{\;}^{2}(R+h)_{\;}^{3}}{G{T}_{2}^{2}}$,故A错误,D正确;
B、地球表面物体重力等于万有引力$mg=G\frac{Mm}{{R}_{\;}^{2}}$,解得$M=\frac{g{R}_{\;}^{2}}{G}$,故B正确;
C、月球绕地球做匀速圆周运动,万有引力提供向心力,有$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{1}^{2}}r$,解得地球质量$M=\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{G{T}_{1}^{2}}$,故C正确;
故选:BCD
点评 解决本题的关键掌握万有引力等于重力和万有引力提供向心力这两个理论,并能灵活运用.

练习册系列答案
相关题目
10. 质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
 质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )| A. | 重力势能增加了mgh | B. | 克服摩擦力做功$\frac{1}{4}$mgh | ||
| C. | 动能损失了mgh | D. | 机械能损失了$\frac{1}{2}$mgh |
6. 如图所示,与水平地面夹角为锐角的下面低端A向上有三个等间距点B、C和D,即AB=BC=CD.小滑块P以初速v从A出发,沿斜面向上运动.先设置斜面与滑块间处处无摩擦,则滑块到达D位置刚好停下,而后下滑.若设置斜面 AB部分与滑块间有处处相同的摩擦,其余部位与滑块间仍无摩擦,则滑块上行到C位置刚好停下,而后下滑.滑块下滑到B位置时速度以及回到 A端时速度大小分别为( )
如图所示,与水平地面夹角为锐角的下面低端A向上有三个等间距点B、C和D,即AB=BC=CD.小滑块P以初速v从A出发,沿斜面向上运动.先设置斜面与滑块间处处无摩擦,则滑块到达D位置刚好停下,而后下滑.若设置斜面 AB部分与滑块间有处处相同的摩擦,其余部位与滑块间仍无摩擦,则滑块上行到C位置刚好停下,而后下滑.滑块下滑到B位置时速度以及回到 A端时速度大小分别为( )
 如图所示,与水平地面夹角为锐角的下面低端A向上有三个等间距点B、C和D,即AB=BC=CD.小滑块P以初速v从A出发,沿斜面向上运动.先设置斜面与滑块间处处无摩擦,则滑块到达D位置刚好停下,而后下滑.若设置斜面 AB部分与滑块间有处处相同的摩擦,其余部位与滑块间仍无摩擦,则滑块上行到C位置刚好停下,而后下滑.滑块下滑到B位置时速度以及回到 A端时速度大小分别为( )
如图所示,与水平地面夹角为锐角的下面低端A向上有三个等间距点B、C和D,即AB=BC=CD.小滑块P以初速v从A出发,沿斜面向上运动.先设置斜面与滑块间处处无摩擦,则滑块到达D位置刚好停下,而后下滑.若设置斜面 AB部分与滑块间有处处相同的摩擦,其余部位与滑块间仍无摩擦,则滑块上行到C位置刚好停下,而后下滑.滑块下滑到B位置时速度以及回到 A端时速度大小分别为( )| A. | $\frac{v}{2}$、$\frac{\sqrt{3}v}{3}$ | B. | $\frac{\sqrt{3}v}{3}$、$\frac{\sqrt{3}v}{3}$ | C. | $\frac{v}{2}$、$\frac{\sqrt{3}v}{2}$ | D. | $\frac{v}{2}$、$\frac{v}{2}$ |
7. 2009年美国重启登月计划,打算在绕月轨道上建造空间站,如图所示,关闭动力的航天飞机在月球引力作用下沿椭圆轨道向月球靠近,并将在P处进入空间站轨道,然后与空间站实验对接.已知空间站绕月轨道半径为r,周期为T,引力常量为G.下列说法中正确的是( )
2009年美国重启登月计划,打算在绕月轨道上建造空间站,如图所示,关闭动力的航天飞机在月球引力作用下沿椭圆轨道向月球靠近,并将在P处进入空间站轨道,然后与空间站实验对接.已知空间站绕月轨道半径为r,周期为T,引力常量为G.下列说法中正确的是( )
 2009年美国重启登月计划,打算在绕月轨道上建造空间站,如图所示,关闭动力的航天飞机在月球引力作用下沿椭圆轨道向月球靠近,并将在P处进入空间站轨道,然后与空间站实验对接.已知空间站绕月轨道半径为r,周期为T,引力常量为G.下列说法中正确的是( )
2009年美国重启登月计划,打算在绕月轨道上建造空间站,如图所示,关闭动力的航天飞机在月球引力作用下沿椭圆轨道向月球靠近,并将在P处进入空间站轨道,然后与空间站实验对接.已知空间站绕月轨道半径为r,周期为T,引力常量为G.下列说法中正确的是( )| A. | 根据题中条件可以算出空间站受到月球引力的大小 | |
| B. | 航天飞机在II轨道上从M向P处运动过程中加速度逐渐变大 | |
| C. | 航天飞机在I轨道过P点的速度比II轨道通过P点的速度小 | |
| D. | 根据题中条件可以算出月球质量 |




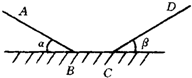 如图所示,一个滑块质量为2kg,从斜面上A点由静止下滑,经过BC平面又冲上另一斜面到达最高点D.已知AB=100cm,CD=60cm,∠α=30°,∠β=37°,且AB、CD均光滑,只有BC面粗糙,BC=28cm且BC面上各处粗糙程度相同,(g取10m/s2)试求:
如图所示,一个滑块质量为2kg,从斜面上A点由静止下滑,经过BC平面又冲上另一斜面到达最高点D.已知AB=100cm,CD=60cm,∠α=30°,∠β=37°,且AB、CD均光滑,只有BC面粗糙,BC=28cm且BC面上各处粗糙程度相同,(g取10m/s2)试求: