题目内容
15. 现要通过实验验证机械能守恒定律.实验装置如图所示:水平桌面上固定-倾斜的气垫导轨;导轨上A点处有一带长方形遮光片的滑块,其总质量为M,左端由跨过轻质光滑定滑轮的细绳与一质量为m的砝码相连;导轨上B点有一光电门,可以测量遮光片经过光电门时的挡光时间t,用d表示A点到导轨低端C点的距离,h表示A与C的高度差,b表示遮光片的宽度,s表示A、B两点的距离,将遮光片通过光电门的平均速度看作滑块通过B点时的瞬时速度.用g表示重力加速度.完成下列填空:若将滑块自A点由静止释放,则在滑块从A运动至B的过程中,滑块、遮光片与砝码组成的系统重力势能的减小量可表示为$(\frac{h}{d}M-m)gs$.动能的增加量可表示为$\frac{1}{2}(m+M)\frac{b^2}{t^2}$.若在运动过程中机械能守恒,$\frac{1}{{t}^{2}}$与s的关系式为$\frac{1}{t^2}=\frac{2(hM-dm)g}{{(M+m)d{b^2}}}s$.
现要通过实验验证机械能守恒定律.实验装置如图所示:水平桌面上固定-倾斜的气垫导轨;导轨上A点处有一带长方形遮光片的滑块,其总质量为M,左端由跨过轻质光滑定滑轮的细绳与一质量为m的砝码相连;导轨上B点有一光电门,可以测量遮光片经过光电门时的挡光时间t,用d表示A点到导轨低端C点的距离,h表示A与C的高度差,b表示遮光片的宽度,s表示A、B两点的距离,将遮光片通过光电门的平均速度看作滑块通过B点时的瞬时速度.用g表示重力加速度.完成下列填空:若将滑块自A点由静止释放,则在滑块从A运动至B的过程中,滑块、遮光片与砝码组成的系统重力势能的减小量可表示为$(\frac{h}{d}M-m)gs$.动能的增加量可表示为$\frac{1}{2}(m+M)\frac{b^2}{t^2}$.若在运动过程中机械能守恒,$\frac{1}{{t}^{2}}$与s的关系式为$\frac{1}{t^2}=\frac{2(hM-dm)g}{{(M+m)d{b^2}}}s$.
分析 关键在于研究对象不是单个物体而是滑块、遮光片与砝码组成的系统.
对于系统的重力势能变化量要考虑系统内每一个物体的重力势能变化量.动能也是一样.
光电门测量瞬时速度是实验中常用的方法.由于光电门的宽度b很小,所以我们用很短时间内的平均速度代替瞬时速度.
解答 解:(1)滑块、遮光片下降重力势能减小,砝码上升重力势能增大.
所以滑块、遮光片与砝码组成的系统重力势能的减小量△EP=Mg$\frac{h}{d}s$-mgs=$(\frac{h}{d}M-m)gs$
光电门测量瞬时速度是实验中常用的方法.由于光电门的宽度b很小,所以我们用很短时间内的平均速度代替瞬时速度.
vB=$\frac{b}{t}$
根据动能的定义式得出:
△Ek=$\frac{1}{2}$(m+M)vB2=$\frac{1}{2}(m+M)\frac{{b}^{2}}{{t}^{2}}$
若在运动过程中机械能守恒,△Ek=△EP;
所以$\frac{1}{t^2}$与s的关系式为$\frac{1}{{t}^{2}}=\frac{2(hM-dm)g}{(M+m)d{b}^{2}}s$
故答案为:$(\frac{h}{d}M-m)gs$;$\frac{1}{2}(m+M)\frac{b^2}{t^2}$;$\frac{1}{t^2}=\frac{2(hM-dm)g}{{(M+m)d{b^2}}}s$.
点评 这个实验对于我们可能是一个新的实验,但该实验的原理都是我们学过的物理规律.
做任何实验问题还是要从最基本的物理规律入手去解决.对于系统问题处理时我们要清楚系统内部各个物体能的变化.

练习册系列答案
相关题目
1.下列说法中正确的是( )
| A. | 物体的两个分运动是直线运动,则它们的合运动一定是直线运动 | |
| B. | 两个互成角度的匀速直线运动的合运动一定是匀速直线运动 | |
| C. | 若汽车驶过拱形桥可以看作圆周运动,则当汽车到达拱桥顶端时汽车处于失重状态 | |
| D. | 做匀速圆周运动的物体其加速度不变,线速度大小也不变 |
3.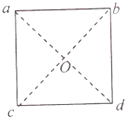 如图所示,一边长为l的正方形,其中a、b、c三个顶点上分别固定了三个电荷量相等的正点电荷Q,O点为正方形的中心,d点为正方形的另一个顶点.下列判定正确的是( )
如图所示,一边长为l的正方形,其中a、b、c三个顶点上分别固定了三个电荷量相等的正点电荷Q,O点为正方形的中心,d点为正方形的另一个顶点.下列判定正确的是( )
 如图所示,一边长为l的正方形,其中a、b、c三个顶点上分别固定了三个电荷量相等的正点电荷Q,O点为正方形的中心,d点为正方形的另一个顶点.下列判定正确的是( )
如图所示,一边长为l的正方形,其中a、b、c三个顶点上分别固定了三个电荷量相等的正点电荷Q,O点为正方形的中心,d点为正方形的另一个顶点.下列判定正确的是( )| A. | O点和d点的场强方向相同 | |
| B. | d点电势比O点的电势高 | |
| C. | 同一试探电荷+q在d点比在O点受到的电场力小 | |
| D. | 同一试探电荷+q在d点比在O点的电势能大 |
10. 如图所示,长为L,质量为m的两导体棒a、b,a被放置在光滑斜面上,b固定在距a为x距离的同一水平面处,且a、b水平平行,设θ=45°,a、b均通以强度为I的同向平等电流时,a恰能在斜面上保持静止,则b的电流在a处所产生的磁场的磁感应强度B的大小为( )
如图所示,长为L,质量为m的两导体棒a、b,a被放置在光滑斜面上,b固定在距a为x距离的同一水平面处,且a、b水平平行,设θ=45°,a、b均通以强度为I的同向平等电流时,a恰能在斜面上保持静止,则b的电流在a处所产生的磁场的磁感应强度B的大小为( )
 如图所示,长为L,质量为m的两导体棒a、b,a被放置在光滑斜面上,b固定在距a为x距离的同一水平面处,且a、b水平平行,设θ=45°,a、b均通以强度为I的同向平等电流时,a恰能在斜面上保持静止,则b的电流在a处所产生的磁场的磁感应强度B的大小为( )
如图所示,长为L,质量为m的两导体棒a、b,a被放置在光滑斜面上,b固定在距a为x距离的同一水平面处,且a、b水平平行,设θ=45°,a、b均通以强度为I的同向平等电流时,a恰能在斜面上保持静止,则b的电流在a处所产生的磁场的磁感应强度B的大小为( )| A. | $\frac{mg}{IL}$ | B. | $\frac{\sqrt{2}mg}{2IL}$ | C. | $\frac{mg}{Ix}$ | D. | $\frac{\sqrt{2}mg}{2Ix}$ |
20.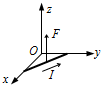 如图,在xOy平面中有一通电直导线与Ox、Oy轴相交,导线中电流方向如图所示.该区域有匀强磁场,通电直导线所受磁场力的方向与Oz轴的正方向相同.该磁场的磁感应强度的方向可能是( )
如图,在xOy平面中有一通电直导线与Ox、Oy轴相交,导线中电流方向如图所示.该区域有匀强磁场,通电直导线所受磁场力的方向与Oz轴的正方向相同.该磁场的磁感应强度的方向可能是( )
 如图,在xOy平面中有一通电直导线与Ox、Oy轴相交,导线中电流方向如图所示.该区域有匀强磁场,通电直导线所受磁场力的方向与Oz轴的正方向相同.该磁场的磁感应强度的方向可能是( )
如图,在xOy平面中有一通电直导线与Ox、Oy轴相交,导线中电流方向如图所示.该区域有匀强磁场,通电直导线所受磁场力的方向与Oz轴的正方向相同.该磁场的磁感应强度的方向可能是( )| A. | 沿x轴正方向 | B. | 沿y轴负方向 | C. | 沿z轴正方向 | D. | 沿z轴负方向 |
7.如图为一物体沿直线运动的速度图象,由此可知( )


| A. | 4s末物体运动方向改变 | B. | 3s末与5s末的速度相同 | ||
| C. | 0-2s与2-4s加速度相同 | D. | 6s末物体的位移为5m |
4. 一带电粒子从电场中的A点运动到B点,轨迹如图中虚线所示,不计粒子所受的重力,实线为电场线,则( )
一带电粒子从电场中的A点运动到B点,轨迹如图中虚线所示,不计粒子所受的重力,实线为电场线,则( )
 一带电粒子从电场中的A点运动到B点,轨迹如图中虚线所示,不计粒子所受的重力,实线为电场线,则( )
一带电粒子从电场中的A点运动到B点,轨迹如图中虚线所示,不计粒子所受的重力,实线为电场线,则( )| A. | 粒子带正电 | B. | 粒子的加速度逐渐增大 | ||
| C. | A点的场强小于B点的场强 | D. | 粒子的速度不断减小 |
5.关于家庭电路中电器安装的说法,错误的是( )
| A. | 开关应接在火线上 | |
| B. | 螺丝口灯泡的螺旋套一定要接在零线上 | |
| C. | 开关应和灯泡并联 | |
| D. | 三孔插座应有接地线 |