题目内容
11. 如图坐标系xOy平面内,以x,y轴为界边长均为L的区域中,有场强大小均为E,方向如图的匀强电场,电场周围有垂直纸面向里的匀强磁场,在第Ⅰ象限内无限接近坐标原点O处有一电荷量为q、质量为m的带正电的粒子,由静止释放后依次分别经Ⅰ、Ⅱ、Ⅲ、Ⅳ象限的电场区域和磁场区域,已知粒子在各个电场区域中均做直线运动,不考虑粒子重力.求:
如图坐标系xOy平面内,以x,y轴为界边长均为L的区域中,有场强大小均为E,方向如图的匀强电场,电场周围有垂直纸面向里的匀强磁场,在第Ⅰ象限内无限接近坐标原点O处有一电荷量为q、质量为m的带正电的粒子,由静止释放后依次分别经Ⅰ、Ⅱ、Ⅲ、Ⅳ象限的电场区域和磁场区域,已知粒子在各个电场区域中均做直线运动,不考虑粒子重力.求:(1)磁场的磁感应强度B的大小;
(2)粒子由静止释放到第一次回到出发点经历的时间t总.
分析 (1)粒子在电场中加速,由动能定理可以求出粒子进入磁场时的速度,粒子在磁场中做匀速圆周运动洛伦兹力通过向心力,由牛顿第二定律可以求出磁感应强度.
(2)分别求出粒子在电场与磁场中的运动时间,然后求出粒子总的运动时间.
解答 解:(1)在电场中由动能定理得:$qEL=\frac{1}{2}m{v^2}$,
由题意可知在磁场中做圆周运动的半径:r=L,
洛伦兹力提供粒子做圆周运动的向心力:$qvB=m\frac{v^2}{r}$,
在电场中由动能定理得:$qEL=\frac{1}{2}m{v^2}$,
解得:B=$\sqrt{\frac{2mE}{qL}}$;
(2)设电场中加速时间为t,磁场中圆周运动的周期为T.
则在电场中,由牛顿第二定律得:qE=ma,
位移:L=$\frac{1}{2}at_{\;}^2$,
解得:$t=\sqrt{\frac{2mL}{qE}}$,
在磁场中粒子做圆周运动的周期:T=$\frac{2πm}{qB}$=2π$\sqrt{\frac{mL}{2qE}}$,
粒子运动的总时间:t总=8t+3T=$(8+3π)\sqrt{\frac{2mL}{qE}}$;
答:(1)磁场的磁感应强度B的大小为$\sqrt{\frac{2mE}{qL}}$;
(2)粒子由静止释放到第一次回到出发点经历的时间t总为$(8+3π)\sqrt{\frac{2mL}{qE}}$.
点评 粒子在电场中做匀变速直线运动,在磁场中做匀速圆周运动,分析清楚粒子运动过程是解题的前提,应用动能定理、牛顿第二定律与运动学公式可以解题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
2. 如图所示,一个宽L=0.20m的“U”型绝缘导轨与水平面成37°倾角固定放置.在导轨区域内存在竖直向下的匀强磁场,磁感应强度B=1.0T.一根质量为0.10kg的金属棒垂直放置在导轨上,棒上通有I=5.0A的电流.金属棒静止,重力加速度g=10m/s2,则( )
如图所示,一个宽L=0.20m的“U”型绝缘导轨与水平面成37°倾角固定放置.在导轨区域内存在竖直向下的匀强磁场,磁感应强度B=1.0T.一根质量为0.10kg的金属棒垂直放置在导轨上,棒上通有I=5.0A的电流.金属棒静止,重力加速度g=10m/s2,则( )
 如图所示,一个宽L=0.20m的“U”型绝缘导轨与水平面成37°倾角固定放置.在导轨区域内存在竖直向下的匀强磁场,磁感应强度B=1.0T.一根质量为0.10kg的金属棒垂直放置在导轨上,棒上通有I=5.0A的电流.金属棒静止,重力加速度g=10m/s2,则( )
如图所示,一个宽L=0.20m的“U”型绝缘导轨与水平面成37°倾角固定放置.在导轨区域内存在竖直向下的匀强磁场,磁感应强度B=1.0T.一根质量为0.10kg的金属棒垂直放置在导轨上,棒上通有I=5.0A的电流.金属棒静止,重力加速度g=10m/s2,则( )| A. | 导轨对金属棒的支持力大小为0.8N | B. | 导轨对金属棒的支持力大小为0.2N | ||
| C. | 导轨对金属棒的摩擦力大小为0.2N | D. | 导轨对金属棒的摩擦力大小为1.4N |
19. 如图所示,理想变压器为降压变压器,原线圈通过灯泡L1与正弦式交流电相连,副线圈通过导线与两个相同的灯泡L2和L3相连,开始时开关S处于断开状态.当S闭合后,所有灯泡都能发光.下列说法中正确的是( )
如图所示,理想变压器为降压变压器,原线圈通过灯泡L1与正弦式交流电相连,副线圈通过导线与两个相同的灯泡L2和L3相连,开始时开关S处于断开状态.当S闭合后,所有灯泡都能发光.下列说法中正确的是( )
 如图所示,理想变压器为降压变压器,原线圈通过灯泡L1与正弦式交流电相连,副线圈通过导线与两个相同的灯泡L2和L3相连,开始时开关S处于断开状态.当S闭合后,所有灯泡都能发光.下列说法中正确的是( )
如图所示,理想变压器为降压变压器,原线圈通过灯泡L1与正弦式交流电相连,副线圈通过导线与两个相同的灯泡L2和L3相连,开始时开关S处于断开状态.当S闭合后,所有灯泡都能发光.下列说法中正确的是( )| A. | 灯泡L1和L2中的电流有效值可能相等 | |
| B. | 灯泡L2两端的电压变小 | |
| C. | 灯泡L1变亮,灯泡L2的亮度不变 | |
| D. | 变压器原线圈的输入功率不变 |


 一标有“6V 0.5 A”的小型直流电动机,转子由铜导线绕制的线圈组成,阻值约为1Ω.某兴趣小组设汁一个实验测量此电动机线圈的电阻.实验室提供的器材除导线和开关外还有:
一标有“6V 0.5 A”的小型直流电动机,转子由铜导线绕制的线圈组成,阻值约为1Ω.某兴趣小组设汁一个实验测量此电动机线圈的电阻.实验室提供的器材除导线和开关外还有:
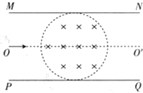 如图所示,平行板MN、PQ间距离为d,板长为2d,板的正中有一半径为$\frac{d}{2}$的圆形有界磁场,磁场边界刚好与两板相切,两板间所加电压为U,一质量为m,电量为q的带电粒子从左端沿两板间的中线向右射入两板间,若只撤去磁场,粒子刚好从上板右端N点射出,若只撤去两板间所加的电压,带电粒子恰好能从下板的右端Q点射出,不计粒子的重力,求:
如图所示,平行板MN、PQ间距离为d,板长为2d,板的正中有一半径为$\frac{d}{2}$的圆形有界磁场,磁场边界刚好与两板相切,两板间所加电压为U,一质量为m,电量为q的带电粒子从左端沿两板间的中线向右射入两板间,若只撤去磁场,粒子刚好从上板右端N点射出,若只撤去两板间所加的电压,带电粒子恰好能从下板的右端Q点射出,不计粒子的重力,求: 如图所示,在与水平方向成60°角的光滑金属导轨间连一电源,在相距1m的平行导轨上放一重为3N的金属棒ab,棒上通以3A的电流,磁场方向竖直向上,这时棒恰好静止,求:
如图所示,在与水平方向成60°角的光滑金属导轨间连一电源,在相距1m的平行导轨上放一重为3N的金属棒ab,棒上通以3A的电流,磁场方向竖直向上,这时棒恰好静止,求: