题目内容
6.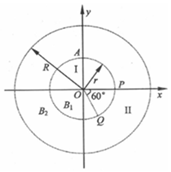 如图所示,原点O为两个大小不同的同心圆的圆心,半径为r的小圆区域Ⅰ内有方向垂直xOy平面向里的匀强磁场,两圆之间的环形区域ⅡII内也有方向垂直于xoy平面的另一匀强磁场.一质量为m、电量为q、初速度为v0的带正电粒子从坐标为(0,r)的A点沿-y方向射入区域I,然后从x轴上的P点沿+x方向射出,粒子经过区域II后从Q点第2次射入区域I,已知OQ与+x方向成60°.角.不计粒子的重力.
如图所示,原点O为两个大小不同的同心圆的圆心,半径为r的小圆区域Ⅰ内有方向垂直xOy平面向里的匀强磁场,两圆之间的环形区域ⅡII内也有方向垂直于xoy平面的另一匀强磁场.一质量为m、电量为q、初速度为v0的带正电粒子从坐标为(0,r)的A点沿-y方向射入区域I,然后从x轴上的P点沿+x方向射出,粒子经过区域II后从Q点第2次射入区域I,已知OQ与+x方向成60°.角.不计粒子的重力.(1)区域I中磁感应强度B1的大小和区域II中磁感应强度B2的大小及方向;
(2)要使粒子约束在磁场内,大圆半径R的最小值;
(3)粒子再次回到坐标A点所经历的最短时间t.
分析 (1)粒子进入磁场Ⅰ做圆周运动,由几何关系求出轨迹半径,由牛顿第二定律求解磁感应强度B1的大小;
(2)在环形区域Ⅱ中,当粒子的运动轨迹与外圆相切,画出轨迹,由几何关系求解轨迹半径,再求解B2的大小.
(3)根据粒子运动的轨迹所对应的圆心角,再求解运动周期和运动的最短时间.
解答 解:(1)设在区域Ⅰ内轨迹圆半径为:r1=r,
粒子在磁场中做圆周运动洛伦兹力提供向心力,
由牛顿第二定律得:qv0B1=m$\frac{{v}_{0}^{2}}{{r}_{1}}$,
解得:B1=$\frac{m{v}_{0}}{qr}$;
(2)粒子在区域Ⅱ中运动轨迹如图所示,由几何关系知:r2=$\frac{\sqrt{3}}{3}$r,
由牛顿第二定律得:qv0B2=m$\frac{{v}_{0}^{2}}{{r}_{2}}$,
解得:B2=$\frac{\sqrt{3}m{v}_{0}}{qr}$,
方向与B1相反,即垂直xoy平面向外;
(2)由几何关系得,大圆半径R的最小值:
R=2r2+r2=3r2,
解得:R=$\sqrt{3}$r;
(3)粒子在磁场中做圆周运动的周期:T1=$\frac{2πm}{q{B}_{1}}$,T2=$\frac{2πm}{q{B}_{2}}$,
轨迹从A点到Q点对应圆心角:θ=90°+60°=150°,要仍从A点沿y轴负方向射入,
需满足:150n=360m,m、n属于自然数,即取最小整数m=5,n=12,
运动时间为:t=12×($\frac{1}{4}$T1+$\frac{2}{3}$T2),
得:t=(6+$\frac{16\sqrt{3}}{3}$)$\frac{πr}{{v}_{0}}$;
答:(1)区域I中磁感应强度B1的大小为:$\frac{m{v}_{0}}{qr}$,区域II中磁感应强度B2的大小为:$\frac{\sqrt{3}m{v}_{0}}{qr}$方向:垂直xoy平面向外;
(2)要使粒子约束在磁场内,大圆半径R的最小值为$\sqrt{3}$r;
(3)粒子再次回到坐标A点所经历的最短时间t为(6+$\frac{16\sqrt{3}}{3}$)$\frac{πr}{{v}_{0}}$.
点评 该题考查带电粒子在磁场中的运动,分析清楚粒子运动过程、作出粒子运动轨迹是解题的前提与关键,应用牛顿第二定律、粒子做圆周运动的周期公式即可解题;处理带电粒子在有界磁场中的运动问题的关键是:作出粒子运动轨迹,确定圆心、求半径与粒子转过的圆心角.

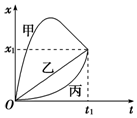
| A. | 甲的平均速度最大 | B. | 乙的平均速度最小 | ||
| C. | 三者的平均速度相同 | D. | 乙的平均速度最大 |
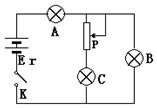
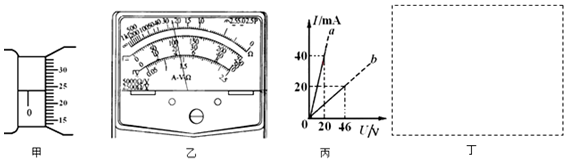
| A. | A灯变亮、B灯变暗、C灯变亮 | B. | A灯变暗、B灯变暗、C灯变亮 | ||
| C. | A灯变亮、B灯变暗、C灯变暗 | D. | A灯变暗、B灯变亮、C灯变暗 |
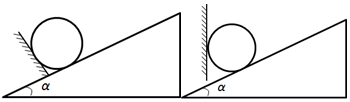
| A. | 2F | B. | 4F | C. | $\frac{1}{2}$F | D. | $\frac{1}{4}$F |
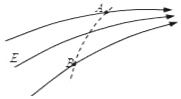 某电场的部分电场线如图所示,A、B是一带电粒子仅在电场力作用下运动轨迹(图中虚线)上的两点,下列说法中正确的是( )
某电场的部分电场线如图所示,A、B是一带电粒子仅在电场力作用下运动轨迹(图中虚线)上的两点,下列说法中正确的是( )| A. | 带点粒子带负电 | |
| B. | 粒子一定是从B点向A点运动 | |
| C. | 电场中A点的电势高于B点的电势 | |
| D. | 粒子在A点的加速度大于它在B点的加速度 |
 如图所示,QA=+3×10-8C,QB=-3×10-8C,A,B两球相距r=5cm,在水平方向外电场作用下,A,B保持静止,悬线竖直,求A,B连线中点场强.(两带电小球可看作质点)静电力常量K=k=9×109 N•m2/C2.
如图所示,QA=+3×10-8C,QB=-3×10-8C,A,B两球相距r=5cm,在水平方向外电场作用下,A,B保持静止,悬线竖直,求A,B连线中点场强.(两带电小球可看作质点)静电力常量K=k=9×109 N•m2/C2.