题目内容
19. 一质量m=2kg物体沿倾角θ=37°的光滑斜面高h=4m无初速的下滑进入半径R=1.6m的竖直光滑圆轨道,且刚好能过圆轨道的最高点,求:
一质量m=2kg物体沿倾角θ=37°的光滑斜面高h=4m无初速的下滑进入半径R=1.6m的竖直光滑圆轨道,且刚好能过圆轨道的最高点,求:(1)物体对圆轨道最低点B的压力是多少?
(2)物体从A点落到斜面的时间?
分析 (1)物块刚好能通过圆轨道最高点时由重力提供向心力,由牛顿第二定律求出物块通过最高点时的速度.物块从B点到A点的过程中,只有重力做功,机械能守恒,由机械能守恒定律求出物块通过B点时的速度,由牛顿运动定律求解物块运动到B点时对圆轨道的压力大小.
(2)物块离开A点后做平抛运动,由平抛运动的规律得到水平位移和竖直位移的表达式,再由几何知识分析它们的关系,即可求时间.
解答 解:(1)物块恰好能运动到圆轨道的最高点A时,由牛顿第二定律得:
mg=m$\frac{{v}_{A}^{2}}{R}$,vA=$\sqrt{gR}$=4m/s
物块从B点到A点的过程中,只有重力做功,机械能守恒,则得
mg•2R+$\frac{1}{2}m{v}_{A}^{2}$=$\frac{1}{2}m{v}_{B}^{2}$
在B点,由牛顿第二定律得:N-mg=m$\frac{{v}_{B}^{2}}{R}$
联立得 N=6mg
根据牛顿第三定律得物体对圆轨道最低点B的压力 N′=N=6mg=6×2×10N=120N
(2)物块离开A点后做平抛运动,落到斜面上时,有:
x=vAt
y=$\frac{1}{2}g{t}^{2}$
又由几何关系有:y+xtanθ=2R
联立得 t=$\frac{\sqrt{73}-3}{10}$s
答:
(1)物体对圆轨道最低点B的压力为120N.
(2)物体从A点落到斜面的时间为$\frac{\sqrt{73}-3}{10}$s.
点评 本题考查了圆周运动和平抛运动的综合,涉及到牛顿第二定律和机械能守恒定律的运用,知道圆周运动最高点的临界条件,找出平抛运动在水平方向和竖直方向上的分位移的关系是解决本题的关键.

练习册系列答案
相关题目
14. 如图,用理想变压器给负载供电,变压器输入电压不变,当负载电阻的滑动端向上移动时,则所有理想交流电表的读数及输入功率P1的变化情况为( )
如图,用理想变压器给负载供电,变压器输入电压不变,当负载电阻的滑动端向上移动时,则所有理想交流电表的读数及输入功率P1的变化情况为( )
 如图,用理想变压器给负载供电,变压器输入电压不变,当负载电阻的滑动端向上移动时,则所有理想交流电表的读数及输入功率P1的变化情况为( )
如图,用理想变压器给负载供电,变压器输入电压不变,当负载电阻的滑动端向上移动时,则所有理想交流电表的读数及输入功率P1的变化情况为( )| A. | V1、V2不变,A1增大,A2减小,P1增大 | |
| B. | V1、V2不变,A1、A2增大,P1增大 | |
| C. | V1、V2不变,A1、A2减小,P1减小 | |
| D. | V1不变,V2增大,A1减小,A2增大,P1减小 |
4.在力学理论建立的过程中有许多伟大的科学家做出了贡献,下列有关科学家和他们的贡献说法错误的是( )
| A. | 伽利略斜面实验合理外推解释了自由落体是匀变速运动 | |
| B. | 开普勒发现了行星运动的规律 | |
| C. | 卡文迪许通过实验测出了引力常量G | |
| D. | 惯性定律是可以被实验直接验证的 |
 如图甲所示,固定在水平桌面上的光滑金属导轨cd、eg处于方向垂直导轨向下的匀强磁场中,金属杆ab与导轨接触良好.在两根导轨的端点C、e之间连接一电阻,其他部分电阻忽略不计.现用一水平向右的外力F1作用在金属杆ab上,使金属杆ab向右沿导轨滑动,滑动过程中金属杆ab始终垂直于导轨.金属杆ab受到的安培力用F2表示,F1与F2随时间t变化的关系图象如图乙所示,下面关于金属杆ab运动过程中的v-t图象不正确的是( )
如图甲所示,固定在水平桌面上的光滑金属导轨cd、eg处于方向垂直导轨向下的匀强磁场中,金属杆ab与导轨接触良好.在两根导轨的端点C、e之间连接一电阻,其他部分电阻忽略不计.现用一水平向右的外力F1作用在金属杆ab上,使金属杆ab向右沿导轨滑动,滑动过程中金属杆ab始终垂直于导轨.金属杆ab受到的安培力用F2表示,F1与F2随时间t变化的关系图象如图乙所示,下面关于金属杆ab运动过程中的v-t图象不正确的是( )



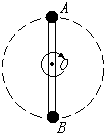 如图所示,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m?,B球质量为2m,两者一起在竖直平面内绕O轴做圆周运动.
如图所示,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m?,B球质量为2m,两者一起在竖直平面内绕O轴做圆周运动.
 ①将条形磁铁按图所示方向插入闭合线圈.在磁铁插入的过程中,灵敏电流表示数不为零.
①将条形磁铁按图所示方向插入闭合线圈.在磁铁插入的过程中,灵敏电流表示数不为零.
 一列简谐横波在x轴上传播,已知t1=0时波形如图中实线所示,t2=0.2s时的波形如图中虚线所示.(横轴上所标数据对应实线与横轴交点)
一列简谐横波在x轴上传播,已知t1=0时波形如图中实线所示,t2=0.2s时的波形如图中虚线所示.(横轴上所标数据对应实线与横轴交点)