题目内容
7. 趣味运动会上有一个项目是在传送带上完成的.如图,A为传送带的左端点,B为右端点,P的正上方天花板上悬挂一个气球,AB间传送带的长度L=31m,P与A的距离L1=9m,传送带以v0=1m/s的恒定速率向左运动.比赛中,挑战者(视为质点)在A点相对地面静止,听到硝声后开始以a1=2m/s2的加速度向右匀加速运动到P,在刺破气球时不慎跌倒,经△t=2s爬起,然后又以a2=1m/s2的加速度,在传送带上匀加速到B点.假设从摔倒至爬起的过程中挑战者与传送带始终相对静止,不计刺破气球的时间,求挑战者从A到达B所需的时间.
趣味运动会上有一个项目是在传送带上完成的.如图,A为传送带的左端点,B为右端点,P的正上方天花板上悬挂一个气球,AB间传送带的长度L=31m,P与A的距离L1=9m,传送带以v0=1m/s的恒定速率向左运动.比赛中,挑战者(视为质点)在A点相对地面静止,听到硝声后开始以a1=2m/s2的加速度向右匀加速运动到P,在刺破气球时不慎跌倒,经△t=2s爬起,然后又以a2=1m/s2的加速度,在传送带上匀加速到B点.假设从摔倒至爬起的过程中挑战者与传送带始终相对静止,不计刺破气球的时间,求挑战者从A到达B所需的时间.
分析 挑战者先向右做匀加速直线运动,然后随着传送带一起向左做匀速直线运动,最后再向右做匀加速直线运动;
对第一次向右匀加速过程,根据位移公式列式求解时间;
对匀速过程根据速度的定义求解向左的位移;
对第2次向右匀加速过程,根据位移公式列式求解时间,得到总时间.
解答 解:取地面为参考系,挑战者从A运动至气球处所用时间为t1,则:
L1=$\frac{1}{2}{a}_{1}{t}_{1}^{2}$ ①
从摔倒到爬起随传送带位移为x1,则:
x1=-v0•△t ②
运动员从爬起到B端位移为x,时间为t2,则:
x=L-L1-x1 ③
$x=-{v}_{0}{t}_{2}+\frac{1}{2}{a}_{2}{t}_{2}^{2}$ ④
挑战者从左端到达右端全过程所需的时间为t,则:
t=t1+△t+t2 ⑤
解得:t=13s
答:挑战者从A到达B所需的时间为13s.
点评 本题关键是明确挑战者的运动性质,然后分三段过程灵活选择运动学公式列式求解,不难.

练习册系列答案
相关题目
17.质量为30kg的小孩坐在秋千板上,小孩离系绳子的横梁3m,如果秋千板摆到最低点时,小孩对秋千板的压力为66ON,他运动速度的大小为(g=10m/s2)( )
| A. | $\sqrt{33}$m/s | B. | 6m/s | C. | $\sqrt{66}$m/s | D. | 4$\sqrt{6}$m/s |
15.下列各运动中,加速度发生变化的是( )
| A. | 匀加速直线运动 | B. | 竖直上抛运动 | C. | 匀速圆周运动 | D. | 平抛运动 |
12. 如图所示,质量为1kg的小球从距地面H=1.6m的A点水平抛出,恰好垂直撞在水平面上半径为1m的半圆形物体上的B点,已知O为半圆的圆心,BO与竖直方向间的夹角为37°,sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,下列说法正确的是( )
如图所示,质量为1kg的小球从距地面H=1.6m的A点水平抛出,恰好垂直撞在水平面上半径为1m的半圆形物体上的B点,已知O为半圆的圆心,BO与竖直方向间的夹角为37°,sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,下列说法正确的是( )
 如图所示,质量为1kg的小球从距地面H=1.6m的A点水平抛出,恰好垂直撞在水平面上半径为1m的半圆形物体上的B点,已知O为半圆的圆心,BO与竖直方向间的夹角为37°,sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,下列说法正确的是( )
如图所示,质量为1kg的小球从距地面H=1.6m的A点水平抛出,恰好垂直撞在水平面上半径为1m的半圆形物体上的B点,已知O为半圆的圆心,BO与竖直方向间的夹角为37°,sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,下列说法正确的是( )| A. | O与A点间的水平距离为2m | B. | 小球平抛的初速度v0为3m/s | ||
| C. | 小球到B点时重力的瞬时功率为40W | D. | 小球从A到B的运动时间为0.4s |





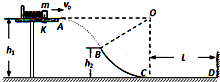 如图,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁定.现接触锁定,小物块与弹簧分离后将以一定的水平速度v0向右从A点滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h2=0.6m,圆弧轨道BC的圆心O与水平台面等高,C点的切线水平,并与长L=2.8m的水平粗糙直轨道CD平滑连接,小物块恰能到达D处.重力加速度g=10m/s2,空气阻力忽略不计.求:
如图,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁定.现接触锁定,小物块与弹簧分离后将以一定的水平速度v0向右从A点滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h2=0.6m,圆弧轨道BC的圆心O与水平台面等高,C点的切线水平,并与长L=2.8m的水平粗糙直轨道CD平滑连接,小物块恰能到达D处.重力加速度g=10m/s2,空气阻力忽略不计.求: 跳台滑雪是勇敢者的运动,运动员在专用滑雪板上,不带雪杖在助滑路上获得高速后水平飞出,在空中飞行一段距离后着陆,这项运动极为壮观.设一位运动员由a点沿水平方向跃起,到山坡b点着陆,如图所示.测得a、b间距离L=40m,山坡倾角θ=30°,山坡可以看成一个斜面.试计算:
跳台滑雪是勇敢者的运动,运动员在专用滑雪板上,不带雪杖在助滑路上获得高速后水平飞出,在空中飞行一段距离后着陆,这项运动极为壮观.设一位运动员由a点沿水平方向跃起,到山坡b点着陆,如图所示.测得a、b间距离L=40m,山坡倾角θ=30°,山坡可以看成一个斜面.试计算: