题目内容
13.绕地球做匀速圆周运动的两颗卫星a、b,已知a的轨道半径大于b的轨道半径,则对于两颗卫星下列说法正确的是( )| A. | a周期大 | B. | a角速度变大 | C. | a速度大 | D. | a向心加速度大 |
分析 根据人造卫星的万有引力等于向心力,列式求出周期、线速度、角速度和向心加速度的表达式,再进行讨论即可.
解答 解:根据人造卫星的万有引力等于向心力,得:
G$\frac{Mm}{{r}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$r=mω2r=m$\frac{{v}^{2}}{r}$=ma
可得 T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,ω=$\sqrt{\frac{GM}{{r}^{3}}}$,v=$\sqrt{\frac{GM}{r}}$,a=$\frac{GM}{{r}^{2}}$,可知卫星的轨道半径越小,角速度、线速度、向心加速度越大,周期越小
由题a的轨道半径大于b的轨道半径,则知a周期大,a角速度、速度和向心加速度都小,故A正确,BCD错误.
故选:A.
点评 本题关键抓住万有引力提供向心力,列式求解出线速度、角速度、周期和向心力的表达式,再进行讨论.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
18.当一个做匀速圆周运动的人造卫星的轨道半径变为原来的2倍时,下列说法正确的是( )
| A. | 卫星的线速度变为原来的$\frac{{\sqrt{2}}}{2}$倍 | B. | 卫星的角速度变为原来的$\frac{{\sqrt{2}}}{2}$倍 | ||
| C. | 卫星所需的向心力变为原来的$\frac{1}{2}$倍 | D. | 卫星的周期变为原来的2$\sqrt{2}$倍 |
5.两个完全相同的电热器,分别通有如图A、B所示的交流电流,则它们的功率之比为( )


| A. | 1:1 | B. | 1:2 | C. | 2:1 | D. | 4:1 |
2.在下列几种运动中遵守机械守恒定律的是( )
| A. | 雨点匀速下落 | |
| B. | 自由落体运动 | |
| C. | 汽车刹车时的运动 | |
| D. | 在光滑水平面上弹簧振子所做的简谐振动 |
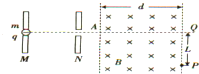 一质量为m,电荷量为q的带电负电离子自静止开始,经M、N两板间的电场加速后,从A点垂直于磁场边界射入宽度为d的匀强磁场中,该粒子离开磁场时的位置P偏离入射方向的距离为L,如图所示,已知M、N两板间的电压为U,粒子的重力不计,求
一质量为m,电荷量为q的带电负电离子自静止开始,经M、N两板间的电场加速后,从A点垂直于磁场边界射入宽度为d的匀强磁场中,该粒子离开磁场时的位置P偏离入射方向的距离为L,如图所示,已知M、N两板间的电压为U,粒子的重力不计,求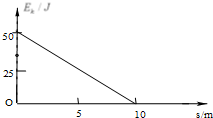 质量为2kg的物体以50J的初动能在粗糙的水平面上滑行,其动能变化与位移的关系如图所示,则物体在水平面上滑行的时间为$2\sqrt{2}$;若该物体以30J的初动能在同一粗糙的水平面上滑行时,其可滑行的最远距离为6m.
质量为2kg的物体以50J的初动能在粗糙的水平面上滑行,其动能变化与位移的关系如图所示,则物体在水平面上滑行的时间为$2\sqrt{2}$;若该物体以30J的初动能在同一粗糙的水平面上滑行时,其可滑行的最远距离为6m. 如图所示是自行车传动部分的结构示意图,牙盘A 通过链条和飞轮B相连,飞轮与后轮C同轴,已知牙盘A、飞轮B和后轮C的半径分别为20cm、10cm、30cm,则当人踩踏脚板使自行车以3m/s的速度在平直的水平路面上匀速前进时,求:
如图所示是自行车传动部分的结构示意图,牙盘A 通过链条和飞轮B相连,飞轮与后轮C同轴,已知牙盘A、飞轮B和后轮C的半径分别为20cm、10cm、30cm,则当人踩踏脚板使自行车以3m/s的速度在平直的水平路面上匀速前进时,求: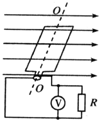 如图所示,匀强磁场的磁感应强度B=0.5T,边长L=10cm的正方形线圈abcd共100匝,此线圈电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO′匀速转动,角速度为ω=2$\sqrt{2}$rad/s,外电路电阻R=4Ω,求:
如图所示,匀强磁场的磁感应强度B=0.5T,边长L=10cm的正方形线圈abcd共100匝,此线圈电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO′匀速转动,角速度为ω=2$\sqrt{2}$rad/s,外电路电阻R=4Ω,求: