题目内容
3.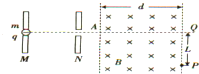 一质量为m,电荷量为q的带电负电离子自静止开始,经M、N两板间的电场加速后,从A点垂直于磁场边界射入宽度为d的匀强磁场中,该粒子离开磁场时的位置P偏离入射方向的距离为L,如图所示,已知M、N两板间的电压为U,粒子的重力不计,求
一质量为m,电荷量为q的带电负电离子自静止开始,经M、N两板间的电场加速后,从A点垂直于磁场边界射入宽度为d的匀强磁场中,该粒子离开磁场时的位置P偏离入射方向的距离为L,如图所示,已知M、N两板间的电压为U,粒子的重力不计,求(1)带电粒子进入匀强磁场时速度的大小v
(2)匀强磁场的磁感应强度的大小B.
分析 (1)粒子在电场中加速,由动能定理可以求出粒子进入磁场时的速度.
(2)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可以求出磁感应强度.
解答 解:(1)设粒子在M、N两板间经电场加速后获得的速度为v,
由动能定理得:qU=$\frac{1}{2}$mv2-0 ①,
解得:v=$\sqrt{\frac{2qU}{m}}$;
(2)粒子进入磁场后做匀速圆周运动,运动轨迹如图所示,设其半径为r,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$ ②,
由几何关系得:r2=(r-L)2+d2 ③,
由①②③解得:B=$\frac{2L}{{L}^{2}+{d}^{2}}$$\sqrt{\frac{2mU}{q}}$;
答:(1)电子进入磁场时的速度为 $\sqrt{\frac{2qU}{m}}$;
(2)匀强磁场的磁感应强度为$\frac{2L}{{L}^{2}+{d}^{2}}$$\sqrt{\frac{2mU}{q}}$.
点评 电子垂直于磁场方向射入磁场后做匀速圆周运动,洛伦兹力提供向心力;由几何知识求出电子轨道半径是求出磁感应强度的关键.

练习册系列答案
相关题目
6. 如图所示是一个小型电风扇电路简图,其中理想变器的原、副线圈的匝数比为22:1,原线圈接电压为U=220V的交流电源,输出端接有一只电阻为R=10Ω的灯泡L和风扇电动机D,电动机线圈电阻为r=2Ω.接通电源后,电风扇正常运转,测出通过风扇电动机的电流为I=1A,则下列说法正确的是( )
如图所示是一个小型电风扇电路简图,其中理想变器的原、副线圈的匝数比为22:1,原线圈接电压为U=220V的交流电源,输出端接有一只电阻为R=10Ω的灯泡L和风扇电动机D,电动机线圈电阻为r=2Ω.接通电源后,电风扇正常运转,测出通过风扇电动机的电流为I=1A,则下列说法正确的是( )
 如图所示是一个小型电风扇电路简图,其中理想变器的原、副线圈的匝数比为22:1,原线圈接电压为U=220V的交流电源,输出端接有一只电阻为R=10Ω的灯泡L和风扇电动机D,电动机线圈电阻为r=2Ω.接通电源后,电风扇正常运转,测出通过风扇电动机的电流为I=1A,则下列说法正确的是( )
如图所示是一个小型电风扇电路简图,其中理想变器的原、副线圈的匝数比为22:1,原线圈接电压为U=220V的交流电源,输出端接有一只电阻为R=10Ω的灯泡L和风扇电动机D,电动机线圈电阻为r=2Ω.接通电源后,电风扇正常运转,测出通过风扇电动机的电流为I=1A,则下列说法正确的是( )| A. | 风扇电动机D两端的电压为2V | |
| B. | 理想变压器的输入功率为10W | |
| C. | 风扇电动机D输出的机械功率为8W | |
| D. | 若电风扇由于机械故障被卡住,则通过原线圈的电流为$\frac{3}{11}$A |
7.下列说法正确的是( )
| A. | 液体的饱和汽压与温度和液体的种类无关 | |
| B. | 在真空、高温条件下,可以利用分子扩散向半导体材料 掺入其它元素 | |
| C. | 晶体熔化时吸收热量,分子平均动能一定增大 | |
| D. | 内能不同的物体,它们的分子热运动的平均动能可能相同 | |
| E. | 物体吸收了热量,其内能不一定增加 |
11.下面给出的四个人物和研究实例中,不符合物理学史的是( )
| A. | 牛顿通过对天体现象的研究,总结出万有引力定律 | |
| B. | 亚里士多德用逻辑推理否定了伽利略关于落体运动的认识 | |
| C. | 欧姆在研究电流与电压、电阻关系时,先保持电阻不变研究电流与电压的关系,然后再保持电压不变研究电流与电阻的关系 | |
| D. | 奥斯特通过放在通电直导线下方的小磁针发生偏转得出通电导线的周围存在磁场的结论 |
8. 半径为r的圆形空间内,存在着垂直于纸面向里的匀强磁场,一个带电粒子(不计重力)从A点以速度v0垂直于磁场方向射入磁场中,并从B点射入,∠AOB=120°,如图所示,则该带电粒子在磁场中( )
半径为r的圆形空间内,存在着垂直于纸面向里的匀强磁场,一个带电粒子(不计重力)从A点以速度v0垂直于磁场方向射入磁场中,并从B点射入,∠AOB=120°,如图所示,则该带电粒子在磁场中( )
 半径为r的圆形空间内,存在着垂直于纸面向里的匀强磁场,一个带电粒子(不计重力)从A点以速度v0垂直于磁场方向射入磁场中,并从B点射入,∠AOB=120°,如图所示,则该带电粒子在磁场中( )
半径为r的圆形空间内,存在着垂直于纸面向里的匀强磁场,一个带电粒子(不计重力)从A点以速度v0垂直于磁场方向射入磁场中,并从B点射入,∠AOB=120°,如图所示,则该带电粒子在磁场中( )| A. | 粒子运动的速度变大 | B. | 粒子运动半径为r | ||
| C. | 粒子运动的时间为$\frac{πr}{3{v}_{0}}$ | D. | 粒子运动的时间为$\frac{\sqrt{3}πr}{3{v}_{0}}$ |
15. 一物体以一定的初速度滑上足够长的斜面.V-t图象如图所示.已知滑块的质量m=0.5kg,斜面的倾角θ=37°,sin37°=0.6,cos37°=0.8,g取10m/s2,则下列说法错误的是( )
一物体以一定的初速度滑上足够长的斜面.V-t图象如图所示.已知滑块的质量m=0.5kg,斜面的倾角θ=37°,sin37°=0.6,cos37°=0.8,g取10m/s2,则下列说法错误的是( )
 一物体以一定的初速度滑上足够长的斜面.V-t图象如图所示.已知滑块的质量m=0.5kg,斜面的倾角θ=37°,sin37°=0.6,cos37°=0.8,g取10m/s2,则下列说法错误的是( )
一物体以一定的初速度滑上足够长的斜面.V-t图象如图所示.已知滑块的质量m=0.5kg,斜面的倾角θ=37°,sin37°=0.6,cos37°=0.8,g取10m/s2,则下列说法错误的是( )| A. | 滑块冲上斜面过程中加速度大小为12m/s2 | |
| B. | 滑块与斜面的动摩擦因素为0.75 | |
| C. | 滑块最后还能返回到斜面底端 | |
| D. | 滑块最后停在斜面上的某个位置 |
13.绕地球做匀速圆周运动的两颗卫星a、b,已知a的轨道半径大于b的轨道半径,则对于两颗卫星下列说法正确的是( )
| A. | a周期大 | B. | a角速度变大 | C. | a速度大 | D. | a向心加速度大 |
 当汽车通过拱桥顶点的速度为10m/s时,车对桥顶的压力为车重$\frac{8}{9}$,如果要使汽车在粗糙的桥面行驶至桥顶时,不受摩擦力作用,则汽车通过桥顶的速度应为多少?
当汽车通过拱桥顶点的速度为10m/s时,车对桥顶的压力为车重$\frac{8}{9}$,如果要使汽车在粗糙的桥面行驶至桥顶时,不受摩擦力作用,则汽车通过桥顶的速度应为多少?