题目内容
质量为m、电量为+q的小球用一绝缘细线悬于O点，开始时它在A、B之间来回摆动，OA、OB与竖直的夹角均为θ，如图所示．（1）如果当它摆到B点时，突然加上一竖直向上、大小为E=mg/q的匀强电场，则此时细线中的拉力F1= ．
（2）如果当它由A摆到最低点C时，突然加上一竖直向上、大小为E=mg/q的匀强电场，则当小球再摆到B点时细线中的拉力F2= ．
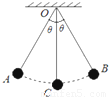
【答案】分析：（1）当小球摆动到B点时，速度为零，加上电场后，电场力与重力平衡，拉力为零；
（2）从A点到C点由动能定理求出C点速度，在最低点根据向心力公式求解拉力．
解答：解析：（1）当小球摆动到B点时，速度为零，向心加速度为零，此时指向圆心的合外力便为零，因为电场力与重力已抵消，故拉力F1=0．
（2）从A点到C点由动能定理可得：
mgl（1-cosθ）=
mv2-0 ①
在最低点C：
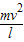F2=
②
联立①②可得：F2=2mg（1-cosθ）．
故答案为：（1）0 （2）2mg（1-cosθ）
点评：本题主要考查了圆周运动向心力公式及动能定理的直接应用，关键要求同学们能正确对小球进行受力分析，难度适中．
（2）从A点到C点由动能定理求出C点速度，在最低点根据向心力公式求解拉力．
解答：解析：（1）当小球摆动到B点时，速度为零，向心加速度为零，此时指向圆心的合外力便为零，因为电场力与重力已抵消，故拉力F1=0．
（2）从A点到C点由动能定理可得：
mgl（1-cosθ）=
mv2-0 ①在最低点C：
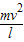F2=
②联立①②可得：F2=2mg（1-cosθ）．
故答案为：（1）0 （2）2mg（1-cosθ）
点评：本题主要考查了圆周运动向心力公式及动能定理的直接应用，关键要求同学们能正确对小球进行受力分析，难度适中．
练习册系列答案
阅读快车系列答案
相关题目
（2012?邯郸模拟）如图所示为某一仪器的部分原理示意图，虚线OA、OB关于y轴对称，且∠AOB=90°，OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域，区域Ⅰ、Ⅲ内存在水平方向的匀强电场，电场强度大小均为E、方向相反．现有质量为m，电量为+q（q＞0）的大量带电粒子从x轴上的粒子源P处以速度v0沿y轴正方向射出，到达OA上的M点时速度与OA垂直．（不计粒子的重力及粒子间的相互作用）求：
如图所示，在xoy平面直角坐标系的第一象限有射线OA，OA与x轴正方向夹角为30°，OA与y轴所夹区域内有沿y轴负方向的匀强电场，其他区域存在垂直于坐标平面向外的匀强磁场．有一质量为m、电量为q的带正电粒子，从y轴上的P点沿着x轴正方向以初速度v0射入电场，运动一段时间后经过Q点垂直于射线OA进入磁场，经磁场偏转，过y轴正半轴上的M点再次垂直进入匀强电场．已知OP=h，不计粒子重力，求：
如图所示，在xoy平面直角坐标系的第一象限有射线OA，OA与x轴正方向夹角为30°，OA与y轴所夹区域内有沿y轴负方向的匀强电场E1，第二象限存在水平向右的匀强电场E2，其它区域存在垂直于坐标平面向外的匀强磁场．有一质量为m、电量为q的带正电粒子，从y轴上的P点沿着x轴正方向以初速度v0射入电场，运动一段时间后经过Q点垂直于射线OA进入磁场，经磁场垂直x轴进入偏转电场E2，过y轴正半轴上的P点再次进入匀强电场E1，已知OP=h，不计粒子重力，求：
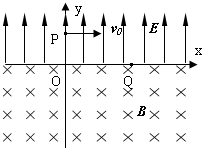如图所示，x轴上方有一匀强电场，方向与y轴平行；x轴下方有一匀强磁场，方向垂直纸面向里．一质量为m、电量为-q（q＞0）的粒子以速度v0从y轴上的P点平行x轴方向射入电场后，从x轴上的Q点进入磁场，并从坐标原点O离开磁场．已知OP=L，OQ=2L．不计重力和一切摩擦，求：