题目内容
11.地球质量约为火星质量的9倍,地球半径为火星半径的2倍,如果地球表面的重力加速度g,火星表面的重力加速度为g′,则g′:g=4:9.在地球表面重力为600N的人到火星表面上的重力变为266.7N.(结果保留一位小数)分析 根据星球表面的万有引力等于重力列出等式表示出重力加速度.
通过火星的质量和半径与地球的关系找出重力加速度的关系,从而可确定重力的关系.
解答 解:解:根据星球表面的万有引力等于重力得出:g=$\frac{GM}{{R}^{2}}$
火星的质量和半径分别约为地球的$\frac{1}{9}$和$\frac{1}{2}$
所以火星表面的重力加速度g′=$\frac{G\frac{1}{9}M}{(\frac{1}{2}R)^{2}}$=$\frac{4}{9}$g 则其比为4:9
地球表面重力为G=600N的人到火星表面其重力为$G′=\frac{4}{9}G$=266.7N
故答案为:4:9 266.7N
点评 求一个物理量之比,我们应该把这个物理量先根据物理规律用已知的物理量表示出来,再进行之比.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
19.关于万有引力定律F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$,下列说法正确的是( )
| A. | 当两物体的距离r趋近于零时,物体间的万有引力F将趋近于无穷大 | |
| B. | 万有引力定律是开普勒发现的 | |
| C. | 引力常量G是英国物理学家卡文迪许测量得出的 | |
| D. | 两个质量分布均匀的分离球体之间的相互作用力可以用F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$来计算,r是两个球心之间的距离 |
3.下列关于万有引力定律的说法,正确的是( )
| A. | 万有引力定律是卡文迪许发现的 | |
| B. | 自然界中的任何两个物体之间都存在万有引力 | |
| C. | 万有引力定律公式F=G$\frac{Mm}{r^2}$中的G是一个比例常数,是没有单位的 | |
| D. | 万有引力定律公式F=G$\frac{Mm}{r^2}$表明当r趋近于零时,万有引力为无穷大 |
20.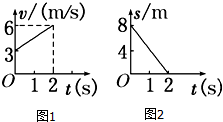 质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )
质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )
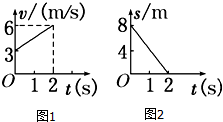 质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )
质量为2kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示,下列说法正确的是( )| A. | 质点的初速度为3 m/s | |
| B. | 2s末质点速度大小为6 m/s | |
| C. | 质点做曲线运动的加速度为1.5m/s2 | |
| D. | 质点初速度的方向与合外力方向垂直 |
1.宇宙中两个相距较近的星球可以看成双星,它们只在相互间的万有引力作用下,绕两球心连线上的某一固定点做周期相同的匀速圆周运动.根据宇宙大爆炸理论,双星间的距离在不断缓慢增加,设双星仍做匀速圆周运动,则下列说法正确的是( )
| A. | 双星做圆周运动的动能均减小 | B. | 双星做圆周运动的半径均增大 | ||
| C. | 双星相互间的万有引力不变 | D. | 双星做圆周运动的角速度均增大 |
 如图所示,竖直平面内的一半径R的光滑圆弧槽BCD,B点与圆心O等高,一水平面与圆弧槽相接于D点.质量m=1.0kg的小球从B点正上方H=0.95m高处的A点自由下落,由B点进入圆弧槽轨道,从D点飞出后落在水平面上的Q点,DQ间的距离x=2.4m,球从D点飞出后的运动过程中相对水平面上升的最大高度h=0.80m,取g=10m/s2,不计空气阻力,求:
如图所示,竖直平面内的一半径R的光滑圆弧槽BCD,B点与圆心O等高,一水平面与圆弧槽相接于D点.质量m=1.0kg的小球从B点正上方H=0.95m高处的A点自由下落,由B点进入圆弧槽轨道,从D点飞出后落在水平面上的Q点,DQ间的距离x=2.4m,球从D点飞出后的运动过程中相对水平面上升的最大高度h=0.80m,取g=10m/s2,不计空气阻力,求: