题目内容
15. 如图中平行金属板中带电质点P原处于静止状态,不考虑电流表和电压表对电路的影响,当滑动变阻器R4的滑片向b端移动时,则( )
如图中平行金属板中带电质点P原处于静止状态,不考虑电流表和电压表对电路的影响,当滑动变阻器R4的滑片向b端移动时,则( )| A. | 电压表读数增大 | B. | 电流表读数增大 | ||
| C. | 质点P将向上运动 | D. | R3上消耗的功率逐渐减小 |
分析 由图可知电路结构,由滑片的移动可知电路中电阻的变化,再由闭合电路欧姆定律可知各电表示数的变化及电容器两端的电压变化;再分析质点的受力情况可知质点的运动情况.
解答 解:A、由图可知,R2与滑动变阻器R4串联后与R3并联后,再与R1串联接在电源两端;电容器与R3并联;
当滑片向b移动时,滑动变阻器接入电阻减小,则电路中总电阻减小;由闭合电路欧姆定律可知,电路中电流增大;路端电压减小,同时R1两端的电压也增大;故并联部分的电压减小;由欧姆定律可知流过R3的电流减小,则流过并联部分的电流增大,故电流表示数增大;因并联部分电压减小,而R2中电压增大,故电压表示数减小,故A错误;B正确;
C、因电容器两端电压减小,故电荷受到的向上电场力减小,则重力大于电场力,合力向下,电荷向下运动,故C错误;
D、因R3两端的电压减小,由P=$\frac{{U}^{2}}{R}$可知,R3上消耗的功率减小; 故D正确;
故选:BD
点评 解决闭合电路欧姆定律的题目,一般可以按照整体-局部-整体的思路进行分析,注意电路中某一部分电阻减小时,无论电路的连接方式如何,总电阻均是减小的.

练习册系列答案
相关题目
6. 如图所示,轻绳相连的两个相同小木块a和b(均可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l.小木块质量为m,木块与圆盘间的动摩擦因数为μ,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,则( )
如图所示,轻绳相连的两个相同小木块a和b(均可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l.小木块质量为m,木块与圆盘间的动摩擦因数为μ,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,则( )
 如图所示,轻绳相连的两个相同小木块a和b(均可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l.小木块质量为m,木块与圆盘间的动摩擦因数为μ,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,则( )
如图所示,轻绳相连的两个相同小木块a和b(均可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l.小木块质量为m,木块与圆盘间的动摩擦因数为μ,重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动,则( )| A. | a与圆盘间的静摩擦力先达到最大值 | |
| B. | 当ω>$\sqrt{\frac{μg}{2l}}$时,绳上出现张力 | |
| C. | 当a、b与圆盘间静摩擦力都达到最大值时,绳上张力为3μmg | |
| D. | 转速太大时,b将远离圆心运动 |
3.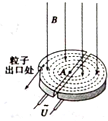 1932年,美国物理学家劳伦斯和利文斯设计出回旋加速器,工作原理示意图如图所示.置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过狭缝的时间可忽略.磁感应强度为B的匀强磁场与盒面垂直,高频交流电频率为f,加速电压为U.若A处粒子源产生的粒子(初速度为0)质量为m、电荷量为+q.在加速器中被加速,加速过程中不考虑重力的影响.则下列说法正确的是( )
1932年,美国物理学家劳伦斯和利文斯设计出回旋加速器,工作原理示意图如图所示.置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过狭缝的时间可忽略.磁感应强度为B的匀强磁场与盒面垂直,高频交流电频率为f,加速电压为U.若A处粒子源产生的粒子(初速度为0)质量为m、电荷量为+q.在加速器中被加速,加速过程中不考虑重力的影响.则下列说法正确的是( )
 1932年,美国物理学家劳伦斯和利文斯设计出回旋加速器,工作原理示意图如图所示.置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过狭缝的时间可忽略.磁感应强度为B的匀强磁场与盒面垂直,高频交流电频率为f,加速电压为U.若A处粒子源产生的粒子(初速度为0)质量为m、电荷量为+q.在加速器中被加速,加速过程中不考虑重力的影响.则下列说法正确的是( )
1932年,美国物理学家劳伦斯和利文斯设计出回旋加速器,工作原理示意图如图所示.置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过狭缝的时间可忽略.磁感应强度为B的匀强磁场与盒面垂直,高频交流电频率为f,加速电压为U.若A处粒子源产生的粒子(初速度为0)质量为m、电荷量为+q.在加速器中被加速,加速过程中不考虑重力的影响.则下列说法正确的是( )| A. | 粒子被加速后的最大速度不可能超过2πRf | |
| B. | 粒子离开回旋加速器时的最大动能与加速电压U成正比 | |
| C. | 粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比为$\sqrt{2}$:1 | |
| D. | 若考虑相对论效应,速率接近光速时粒子的质量会随速率有显著增加 |
10. 将两个质量均为m的小球a、b用细线相连并悬挂于O点,用力F拉小球a,使整个装置处于静止状态,且悬线L与竖直方向的夹角θ=30°,则力F的大小( )
将两个质量均为m的小球a、b用细线相连并悬挂于O点,用力F拉小球a,使整个装置处于静止状态,且悬线L与竖直方向的夹角θ=30°,则力F的大小( )
 将两个质量均为m的小球a、b用细线相连并悬挂于O点,用力F拉小球a,使整个装置处于静止状态,且悬线L与竖直方向的夹角θ=30°,则力F的大小( )
将两个质量均为m的小球a、b用细线相连并悬挂于O点,用力F拉小球a,使整个装置处于静止状态,且悬线L与竖直方向的夹角θ=30°,则力F的大小( )| A. | 可能为$\frac{\sqrt{3}mg}{3}$ | B. | 可能为3mg | C. | 可能为$\frac{2\sqrt{3}mg}{3}$ | D. | 不可能为$\sqrt{2}$mg |
20.将一小球从P点水平抛出,落在水平地面时速度方向与水平方向的夹角为θ,P点离水平地面的高度为h,重力加速度为g,则( )
| A. | 小球的质量可以求出 | B. | 小球抛出时的速度可以求出 | ||
| C. | 小球在空中运动的时间可以求出 | D. | 小球落地时的速度大小无法求出 |
4. 如图,长为L的细绳一端系在天花板上的O点,另一端系一质量m的小球.将小球拉至细绳处于水平的位置由静止释放,在小球沿圆弧从A运动到B的过程中,不计阻力,则( )
如图,长为L的细绳一端系在天花板上的O点,另一端系一质量m的小球.将小球拉至细绳处于水平的位置由静止释放,在小球沿圆弧从A运动到B的过程中,不计阻力,则( )
 如图,长为L的细绳一端系在天花板上的O点,另一端系一质量m的小球.将小球拉至细绳处于水平的位置由静止释放,在小球沿圆弧从A运动到B的过程中,不计阻力,则( )
如图,长为L的细绳一端系在天花板上的O点,另一端系一质量m的小球.将小球拉至细绳处于水平的位置由静止释放,在小球沿圆弧从A运动到B的过程中,不计阻力,则( )| A. | 小球经过B点时,小球的动能为mgL | |
| B. | 小球经过B点时,绳子的拉力为3mg | |
| C. | 小球下摆过程中,重力对小球做功的平均功率为0 | |
| D. | 小球下摆过程中,重力对小球做功的瞬时功率先增大后减小 |
5. 如图所示,穿在一根光滑固定杆上的两个小球A、B连接在一条跨过定滑轮的细绳两端,杆与水平面成θ角,不计所有摩擦.当两球静止时,OA绳与杆的夹角也为θ,OB绳沿竖直方向,则下列说法正确的是( )
如图所示,穿在一根光滑固定杆上的两个小球A、B连接在一条跨过定滑轮的细绳两端,杆与水平面成θ角,不计所有摩擦.当两球静止时,OA绳与杆的夹角也为θ,OB绳沿竖直方向,则下列说法正确的是( )
 如图所示,穿在一根光滑固定杆上的两个小球A、B连接在一条跨过定滑轮的细绳两端,杆与水平面成θ角,不计所有摩擦.当两球静止时,OA绳与杆的夹角也为θ,OB绳沿竖直方向,则下列说法正确的是( )
如图所示,穿在一根光滑固定杆上的两个小球A、B连接在一条跨过定滑轮的细绳两端,杆与水平面成θ角,不计所有摩擦.当两球静止时,OA绳与杆的夹角也为θ,OB绳沿竖直方向,则下列说法正确的是( )| A. | 球B受到3个力作用 | |
| B. | 绳子对球A的拉力大于对球B的拉力 | |
| C. | 球A、B的质量之比为1:tanθ | |
| D. | 若将球B沿杆向上移动少许,则系统在新的位置仍能保持平衡 |
 如图所示,两端封闭的玻璃管中间有一段长为h=16cm的水银柱,在27℃的室内水平放置,水银柱把玻璃管中的气体分成长度都是L0=40cm的A、B两部分,两部分气体的压强均为p0=30cmHg.现将A端抬起使玻璃管竖直
如图所示,两端封闭的玻璃管中间有一段长为h=16cm的水银柱,在27℃的室内水平放置,水银柱把玻璃管中的气体分成长度都是L0=40cm的A、B两部分,两部分气体的压强均为p0=30cmHg.现将A端抬起使玻璃管竖直