题目内容
19.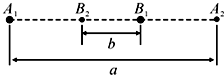 在天文观测中,因为观测视角的问题,有时会看到一种比较奇怪的“双星”系统:与其它天体相距很远的两颗恒星,在同一直线上往返运动,它们往返运动的中心相同,周期也一样.模型如图所示,恒星A在A1A2之间往返运动,恒星B在B1B2之间往返运动,且A1A2=a,B1B2=b,现观测得它们运动的周期为T,恒星A、B的质量分别为M、m,万有引力常量G,则( )
在天文观测中,因为观测视角的问题,有时会看到一种比较奇怪的“双星”系统:与其它天体相距很远的两颗恒星,在同一直线上往返运动,它们往返运动的中心相同,周期也一样.模型如图所示,恒星A在A1A2之间往返运动,恒星B在B1B2之间往返运动,且A1A2=a,B1B2=b,现观测得它们运动的周期为T,恒星A、B的质量分别为M、m,万有引力常量G,则( )| A. | M+m=$\frac{{4π^2{({a+b})}^3}}{GT^2}$ | B. | M+m=$\frac{{π^2{({a+b})}^3}}{2GT^2}$ | ||
| C. | M+m=$\frac{{π^2{({a-b})}^3}}{2GT^2}$ | D. | M+m=$\frac{π^2(a^3+b^3)}{2GT^2}$ |
分析 两颗恒星做的均为圆周运动,所给的距离为运动的直径,即运动的半径及周期可知,由万有引力提供向心力可确定质量之和.
解答 解:对于B的运动:$\frac{GMm}{(\frac{a+b}{2})^{2}}$=m$\frac{b}{2}\frac{4{π}^{2}}{{T}^{2}}$ ①
对于A的运动:$\frac{GMm}{(\frac{a+b}{2})^{2}}$=$M\frac{a}{2}\frac{4{π}^{2}}{{T}^{2}}$ ②
由①②可得:M+m=$\frac{{π^2{({a+b})}^3}}{2GT^2}$ 则B正确,ACD错误.
故选:B
点评 明确看到的为直线但实际运动为圆周,并且由万有引力提供向心力进行求得质量.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
9.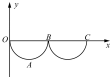 如图所示,xOy坐标平面在竖直面内,y轴正方向竖直向上,空间有垂直于xOy平面的匀强磁场(图中未画出).一带电小球从O点由静止释放,运动轨迹如图中曲线所示,下列说法正确有是( )
如图所示,xOy坐标平面在竖直面内,y轴正方向竖直向上,空间有垂直于xOy平面的匀强磁场(图中未画出).一带电小球从O点由静止释放,运动轨迹如图中曲线所示,下列说法正确有是( )
 如图所示,xOy坐标平面在竖直面内,y轴正方向竖直向上,空间有垂直于xOy平面的匀强磁场(图中未画出).一带电小球从O点由静止释放,运动轨迹如图中曲线所示,下列说法正确有是( )
如图所示,xOy坐标平面在竖直面内,y轴正方向竖直向上,空间有垂直于xOy平面的匀强磁场(图中未画出).一带电小球从O点由静止释放,运动轨迹如图中曲线所示,下列说法正确有是( )| A. | 洛伦兹力可能做了功 | |
| B. | 小球在整个运动过程中机械能增加 | |
| C. | 小球在A点时受到的洛伦兹力与重力大小相等 | |
| D. | 小球运动至最低点A时速度最大,且沿水平方向 |
10. 如图甲所示,物体受到水平推力F的作用在粗糙水平面上做直线运动.通过力传感器和速度传感器监测到推力F、物体速度v随时间t变化的规律如图乙所示.取g=10m/s2.则( )
如图甲所示,物体受到水平推力F的作用在粗糙水平面上做直线运动.通过力传感器和速度传感器监测到推力F、物体速度v随时间t变化的规律如图乙所示.取g=10m/s2.则( )
 如图甲所示,物体受到水平推力F的作用在粗糙水平面上做直线运动.通过力传感器和速度传感器监测到推力F、物体速度v随时间t变化的规律如图乙所示.取g=10m/s2.则( )
如图甲所示,物体受到水平推力F的作用在粗糙水平面上做直线运动.通过力传感器和速度传感器监测到推力F、物体速度v随时间t变化的规律如图乙所示.取g=10m/s2.则( )| A. | 物体的质量m=1.0 kg | |
| B. | 物体与水平面间的动摩擦因数μ=0.20 | |
| C. | 第2 s内物体克服摩擦力做的功W=2.0 J | |
| D. | 前2 s内推力F做功的平均功率$\overline{P}$=1.5 W |
14.一质点做匀速圆周运动,其线速度大小为4m/s,转动周期为2s,则下列判断不正确的是( )
| A. | 角速度为0.5rad/s | B. | 转速为0.5r/s | ||
| C. | 轨迹半径为$\frac{4}{π}$m | D. | 加速度大小为4πm/s2 |
4.小球每隔0.2s从同一高度抛出,做初速为6m/s的竖直上抛运动,设它们在空中不相碰.第一个小球在抛出点以上能遇到的小球数为(取 g=10m/s2)( )
| A. | 3 个 | B. | 4 个 | C. | 5 个 | D. | 6 个 |
11.关于气体热现象的微观解释,下列说法中正确的是( )
| A. | 气体分子的运动杂乱无章,在某一时刻,向着任何一个方向运动的分子都有,而且向各个方向运动的气体分子数目都相等 | |
| B. | 大量气体分子做无规则运动,速率有大有小,但是分子的速率按“中间少,两头多”的规律分布 | |
| C. | 一定质量的某种理想气体,温度升高时,分子的平均动能增大,气体的压强一定增大 | |
| D. | 两个相同的半球壳密闭接触,中间抽成真空(马德堡半球)后,很难用力将之拉开,这是分子间存在吸引力的宏观表现 | |
| E. | 高空中的冰晶在空气中下落变成雨滴时内能增加了 | |
| F. | 任何热机都不可能使燃料释放的热量全部转化为机械能而不引起其它变化 |
8. 如图1所示,小物体从竖直弹簧上方离地高h1处 由静止释放,其动能Ek与离地高度h的关系如图2所示.其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,弹簧的重力不计.小物体质量为m,重力加速度为g.以下说法正确的是( )
如图1所示,小物体从竖直弹簧上方离地高h1处 由静止释放,其动能Ek与离地高度h的关系如图2所示.其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,弹簧的重力不计.小物体质量为m,重力加速度为g.以下说法正确的是( )
 如图1所示,小物体从竖直弹簧上方离地高h1处 由静止释放,其动能Ek与离地高度h的关系如图2所示.其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,弹簧的重力不计.小物体质量为m,重力加速度为g.以下说法正确的是( )
如图1所示,小物体从竖直弹簧上方离地高h1处 由静止释放,其动能Ek与离地高度h的关系如图2所示.其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,弹簧的重力不计.小物体质量为m,重力加速度为g.以下说法正确的是( )| A. | 小物体下降至高度h2时,弹簧的弹性势能为0 | |
| B. | 小物体下落至高度h3时,弹簧的弹性势能最大 | |
| C. | 小物体下落至高度h3时,弹簧的弹性势能最小 | |
| D. | 小物体从高度h1下降到h5,弹簧的弹性势能为mg(h1-h5) |
 如图所示,在光滑水平面上,有足够长度的木板B,质量为mB=4kg,其上有一滑块C,质量为mC=4kg,B、C之间的动摩擦因数为0.2.现有质量为mA=lkg的滑块A,以v0=12m/s的初速度向B运动,与B碰撞(碰撞时间极短)后以4m/s速度弹回.求:
如图所示,在光滑水平面上,有足够长度的木板B,质量为mB=4kg,其上有一滑块C,质量为mC=4kg,B、C之间的动摩擦因数为0.2.现有质量为mA=lkg的滑块A,以v0=12m/s的初速度向B运动,与B碰撞(碰撞时间极短)后以4m/s速度弹回.求: