题目内容
4.小球每隔0.2s从同一高度抛出,做初速为6m/s的竖直上抛运动,设它们在空中不相碰.第一个小球在抛出点以上能遇到的小球数为(取 g=10m/s2)( )| A. | 3 个 | B. | 4 个 | C. | 5 个 | D. | 6 个 |
分析 小球做竖直上抛运动,先求解出小球在空中运动的总时间,然后判断小球在抛出点以上能遇到的小球数.
解答 解:小球做竖直上抛运动,从抛出到落地的整个过程是匀变速运动,在空中运动的总时间为:
t=$\frac{2{v}_{0}}{g}$=$\frac{2×6}{10}$s=1.2s
每隔0.2s抛出一个小球,故第一个小球在抛出点以上能遇到的小球数为:N=$\frac{t}{T}$-1=5(个),故ABD错误,C正确.
故选:C
点评 本题关键明确第一个小球的运动情况,然后选择恰当的运动学公式列式求解出运动时间,再判断相遇的小球个数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.2015年,我国科学家实现了量子瞬间传输技术的重大突破,迈出了实现远距离、大信息的量子信息传输的关键一步,下列学说属于量子理论范畴的是 ( )
| A. | 普朗克电磁辐射理论 | B. | 卢瑟福原子核式结构理论 | ||
| C. | 麦克斯韦光的电磁说 | D. | 爱因斯坦光电效应理论 |
19.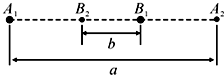 在天文观测中,因为观测视角的问题,有时会看到一种比较奇怪的“双星”系统:与其它天体相距很远的两颗恒星,在同一直线上往返运动,它们往返运动的中心相同,周期也一样.模型如图所示,恒星A在A1A2之间往返运动,恒星B在B1B2之间往返运动,且A1A2=a,B1B2=b,现观测得它们运动的周期为T,恒星A、B的质量分别为M、m,万有引力常量G,则( )
在天文观测中,因为观测视角的问题,有时会看到一种比较奇怪的“双星”系统:与其它天体相距很远的两颗恒星,在同一直线上往返运动,它们往返运动的中心相同,周期也一样.模型如图所示,恒星A在A1A2之间往返运动,恒星B在B1B2之间往返运动,且A1A2=a,B1B2=b,现观测得它们运动的周期为T,恒星A、B的质量分别为M、m,万有引力常量G,则( )
 在天文观测中,因为观测视角的问题,有时会看到一种比较奇怪的“双星”系统:与其它天体相距很远的两颗恒星,在同一直线上往返运动,它们往返运动的中心相同,周期也一样.模型如图所示,恒星A在A1A2之间往返运动,恒星B在B1B2之间往返运动,且A1A2=a,B1B2=b,现观测得它们运动的周期为T,恒星A、B的质量分别为M、m,万有引力常量G,则( )
在天文观测中,因为观测视角的问题,有时会看到一种比较奇怪的“双星”系统:与其它天体相距很远的两颗恒星,在同一直线上往返运动,它们往返运动的中心相同,周期也一样.模型如图所示,恒星A在A1A2之间往返运动,恒星B在B1B2之间往返运动,且A1A2=a,B1B2=b,现观测得它们运动的周期为T,恒星A、B的质量分别为M、m,万有引力常量G,则( )| A. | M+m=$\frac{{4π^2{({a+b})}^3}}{GT^2}$ | B. | M+m=$\frac{{π^2{({a+b})}^3}}{2GT^2}$ | ||
| C. | M+m=$\frac{{π^2{({a-b})}^3}}{2GT^2}$ | D. | M+m=$\frac{π^2(a^3+b^3)}{2GT^2}$ |
16.某物体沿与水平面成30°的木板恰好能匀速下滑;现将该木板与水平面的夹角调整为60°,并使该物体以某一初速度沿该木板向上滑动,则该物体上滑过程中的加速度大小为(取g=10m/s2)( )
| A. | $\frac{{20\sqrt{3}}}{3}$m/s2 | B. | $\frac{{10\sqrt{3}}}{3}$m/s2 | C. | $\frac{{5\sqrt{3}}}{3}$m/s2 | D. | $5\sqrt{3}$m/s2 |
13.以下关于光的说法正确的是( )
| A. | 光纤通信是利用了全反射的原理 | |
| B. | 无色肥皂液吹出的肥皂泡呈彩色是由于光照射时发生了薄膜干涉 | |
| C. | 人们眯起眼睛看灯丝时看到的彩色条纹是光的偏振现象 | |
| D. | 麦克斯韦提出光是一种电磁波并通过实验证实了电磁波的存在 |
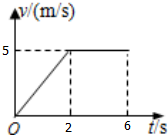 物体做直线运动的v-t图象如图所示,则该物体在前2秒内的加速度大小为2.5m/s2;在第2秒末~第6秒末时间内处于匀速状态(选填“匀速”、“静止”或“匀加速”).
物体做直线运动的v-t图象如图所示,则该物体在前2秒内的加速度大小为2.5m/s2;在第2秒末~第6秒末时间内处于匀速状态(选填“匀速”、“静止”或“匀加速”). 如图所示,四分之一圆柱体玻璃砖半径R=8cm,放在水平地面上,一束激光平行于OB从OA上C点射入玻璃砖,恰好从玻璃砖的曲面上D点射出,最后激光打在水平地面上E点,BE=2cm,求:
如图所示,四分之一圆柱体玻璃砖半径R=8cm,放在水平地面上,一束激光平行于OB从OA上C点射入玻璃砖,恰好从玻璃砖的曲面上D点射出,最后激光打在水平地面上E点,BE=2cm,求:
 如图所示,水平传送带以v0=6m/s顺时针匀速转动,长为6m,右端与光滑竖直半圆弧轨道平滑对接,圆弧轨道的半径R=0.5m,O为圆心,最高点C正下方有一挡板OD,CD间距略大于物块大小,平台OE足够长,现将质量为m=1kg的物块轻放在传送带的最左端A处,物块(可视为质点)与传送带间的动摩擦因数μ=0.5,g取10m/s2.
如图所示,水平传送带以v0=6m/s顺时针匀速转动,长为6m,右端与光滑竖直半圆弧轨道平滑对接,圆弧轨道的半径R=0.5m,O为圆心,最高点C正下方有一挡板OD,CD间距略大于物块大小,平台OE足够长,现将质量为m=1kg的物块轻放在传送带的最左端A处,物块(可视为质点)与传送带间的动摩擦因数μ=0.5,g取10m/s2.