题目内容
2. 如图所示为一架小型四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.现进行试验,设无人机的质量为m=4kg,运动过程中所受空气阻力大小恒为f=4N,当无人机在地面上从静止开始以最大升力竖直向上起飞,经时间t=4s时离地面的高度为h=48m,g取10m/s2.求:
如图所示为一架小型四旋翼无人机,它是一种能够垂直起降的小型遥控飞行器,目前正得到越来越广泛的应用.现进行试验,设无人机的质量为m=4kg,运动过程中所受空气阻力大小恒为f=4N,当无人机在地面上从静止开始以最大升力竖直向上起飞,经时间t=4s时离地面的高度为h=48m,g取10m/s2.求:(1)其动力系统所能提供的最大升力为多大?
(2)无人机通过调整升力继续上升,恰能悬停在距离地面高度为H=118m处,求无人机从h上升到H的过程中,动力系统所做的功为多大?
(3)当无人机悬停在距离地面高度H=118m处时,突然关闭动力设备,无人机从静止开始竖直坠落,经2s后无人机瞬间又恢复最大升力,则无人机在下落过程中距地面的最低高度为多大?
分析 (1)根据匀变速直线运动的位移时间公式求出加速度,结合牛顿第二定律求出最大升力的大小.
(2)先求出t=4s时的速度,无人机从h上升到H的过程中,根据动能定理求动力系统所做的功;
(3)根据牛顿第二定律求出无人机失去升力下落的加速度和位移,恢复升力后的加速度和位移,最后求出无人机在下落过程中距地面的最低高度;
解答 解:(1)由位移公式得:$h=\frac{1}{2}{a}_{1}^{\;}{t}_{\;}^{2}$
${a}_{1}^{\;}=\frac{2h}{{t}_{\;}^{2}}=6m/{s}_{\;}^{2}$
由牛顿第二定律得:F-mg-f=ma1
F=68N
(2)v1=a1t=24m/s,
根据动能定理有:$W-(mg+f)(H-h)=0-\frac{1}{2}m{v}_{1}^{2}$
解得:W=1928J
(3)失去升力后下落过程:$mg-f=m{a_2},{a_2}=9m/{s^2}$,
经过2s后速度v1=a2t1=18m/s,下落高度${h_1}=\frac{1}{2}{a_2}t_1^2=18m$,
恢复升力后减速下降:$F-mg+f=m{a}_{3}^{\;}$
${a}_{3}^{\;}=8m/{s}_{\;}^{2}$
根据速度位移关系有:${v}_{1}^{2}-0=2{a}_{3}^{\;}{h}_{2}^{\;}$
h2=20.25m
故无人机下落时距地面的最低高度△H=H-(h1+h2)=79.75m
答:(1)其动力系统所能提供的最大升力为68N
(2)无人机从h上升到H的过程中,动力系统所做的功为1928J
(3)则无人机在下落过程中距地面的最低高度为20.25m
点评 本题的关键是对飞行器的受力分析以及运动情况的分析,结合牛顿第二定律和运动学基本公式求解,本题难度适中.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 2015年12月6日,载人飞行包在中国深圳实现了首次载人飞行,载人飞行包是一个单人飞行装置,其发动机使用汽油作为燃料提供动力,可以垂直起降,也可以快速前进,对飞行包(包括人)在下列运动过程中(空气阻力不可忽略)的说法,正确的是( )
2015年12月6日,载人飞行包在中国深圳实现了首次载人飞行,载人飞行包是一个单人飞行装置,其发动机使用汽油作为燃料提供动力,可以垂直起降,也可以快速前进,对飞行包(包括人)在下列运动过程中(空气阻力不可忽略)的说法,正确的是( )| A. | 垂直缓慢降落,动力大小大于总重力 | |
| B. | 水平匀速飞行,动力大小等于总重力 | |
| C. | 垂直加速起飞,动力做的功大于克服空气阻力做的功 | |
| D. | 水平加速前进,动力方向与运动方向相同 |
 为验证动能定理,某同学设计了如下实验.将一长直木板一端垫起,另一端侧面装一速度传感器,让小滑块由静止从木板h高处(从传感器所在平面算起)自由滑下至速度传感器时,读出滑块经此处时的速度v,如图所示.多次改变滑块的下滑高度h(斜面的倾角不变),对应的速度值记录在表中:
为验证动能定理,某同学设计了如下实验.将一长直木板一端垫起,另一端侧面装一速度传感器,让小滑块由静止从木板h高处(从传感器所在平面算起)自由滑下至速度传感器时,读出滑块经此处时的速度v,如图所示.多次改变滑块的下滑高度h(斜面的倾角不变),对应的速度值记录在表中:| 下滑高度h/m | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 |
| 速度v/m•s-1 | 0.633 | 0.895 | 1.100 | 1.265 | 1.414 |
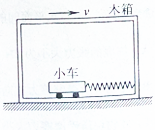 如图所示,质量为2kg的木箱以2m/s2的加速度水平向右做匀加速运动,在箱内有一劲度系数为50N/m的轻弹簧,其一被固定在箱子的右侧壁,另一端拴接一个质量为1kg的小车,木箱与小车相对静止,如图所示.不计小车与木箱之间的摩擦,则( )
如图所示,质量为2kg的木箱以2m/s2的加速度水平向右做匀加速运动,在箱内有一劲度系数为50N/m的轻弹簧,其一被固定在箱子的右侧壁,另一端拴接一个质量为1kg的小车,木箱与小车相对静止,如图所示.不计小车与木箱之间的摩擦,则( )| A. | 弹簧被压缩8cm | B. | 弹簧被压缩4cm | C. | 弹簧被拉伸8cm | D. | 弹簧被拉伸4cm |
 如图所示,在光滑水平面上,轻质弹簧的右端固定在竖直墙壁上,一物块在水平恒力F作用下做直线运动,接触弹簧后压缩弹簧,直至速度为零.整个过程中,物体一直受到力F作用,弹簧一直在弹性限度内.在物块与弹簧接触后向右运动的过程中,下列说法正确的是( )
如图所示,在光滑水平面上,轻质弹簧的右端固定在竖直墙壁上,一物块在水平恒力F作用下做直线运动,接触弹簧后压缩弹簧,直至速度为零.整个过程中,物体一直受到力F作用,弹簧一直在弹性限度内.在物块与弹簧接触后向右运动的过程中,下列说法正确的是( )| A. | 物块接触弹簧后立即做减速运动 | |
| B. | 物块接触弹簧后先加速后减速 | |
| C. | 当物块的速度最大时,它的加速度等于零 | |
| D. | 当弹簧形变量最大时,物块的加速度等于零 |
 如图所示,质量为5kg的物块和小车均处于静止状态,物块与一被水平拉伸的轻弹簧拴接,弹簧的弹力为5N,若小车以2m/s2的加速度向右运动后,则(g=10m/s2)( )
如图所示,质量为5kg的物块和小车均处于静止状态,物块与一被水平拉伸的轻弹簧拴接,弹簧的弹力为5N,若小车以2m/s2的加速度向右运动后,则(g=10m/s2)( )| A. | 物体相对小车向左运动 | B. | 物体受到的摩擦力减小 | ||
| C. | 物体受到的摩擦力大小不变 | D. | 物体受到的弹簧拉力增大 |
 如图所示,一理想变压器的原副线圈匝数比为n1:n2=10:1,一阻值为10Ω的电阻R连接在变压器的副线圈上.若加在原线圈上的电压瞬时值随时间变化规律为u=100$\sqrt{2}$cosl00πt(V),下列说法中正确的是( )
如图所示,一理想变压器的原副线圈匝数比为n1:n2=10:1,一阻值为10Ω的电阻R连接在变压器的副线圈上.若加在原线圈上的电压瞬时值随时间变化规律为u=100$\sqrt{2}$cosl00πt(V),下列说法中正确的是( )| A. | 电压表的示数为10$\sqrt{2}$V | B. | 变压器的输入功率为10W | ||
| C. | 电流表的示数为0.1 A | D. | 交变电流的频率为100 Hz |
 测量电阻一般用伏安法、但有时也用其它方法,为了较精确地测量电阻Rx(约300Ω)的值,请同学们在现有下列器材作出选择.
测量电阻一般用伏安法、但有时也用其它方法,为了较精确地测量电阻Rx(约300Ω)的值,请同学们在现有下列器材作出选择. 如图所示,将导轨、可移动导体AB放置在磁场中,并和电流计组成闭合回路.注意在下列情况下电路中是否有电流产生.
如图所示,将导轨、可移动导体AB放置在磁场中,并和电流计组成闭合回路.注意在下列情况下电路中是否有电流产生.