题目内容
2.如图所示,绝缘平板S放在水平地面上,S与水平面间的动摩擦因数μ=0.4.两块足够大的平行金属板P、Q通过导体支架连接并固定在S上.在两极板之间有垂直纸面向里的足够大匀强磁场,磁感应强度为B=1T.P板的中央有一小孔,整个装置的总质量为M=3.6kg.给装置施加水平向右的作用力,使其总是以恒定的速度v=6m/s向右匀速运动,同时将一质量为m=0.4kg的带负电的小球,从离P板高h=1.25m处由静止释放,小球恰好能落入孔内.若小球进入小孔后做匀速圆周运动,且恰好不与Q板接触,之后又返回P板(不计空气阻力,不考虑运动产生的磁场,g取10m/s2,π取3).求: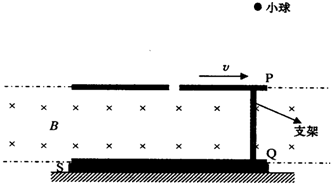
(1)小球所带电荷量;
(2)小球进入两极板间后,水平向右的作用力F;
(3)小球返回打到P板的位置到小孔的距离.
分析 (1)根据法拉第电磁感应定律求出金属支架运动切割磁感线产生的感应电动势,电动势等于两极板间的电压,求出两板间场强,根据小球的受力平衡求小球的电量
(2)小球进入磁场后,对金属板受力分析,水平向右的作用力和滑动摩擦力平衡,求出拉力F
(3)小球在板间做匀速圆周运动,返回到P板,时间是半个周期,求出在此时间内金属板向右匀速直线运动的位移,求出小球匀速圆周运动的半径和周期,根据几何关系即可得到小球返回打到P板的位置到小孔的距离
解答 (1)设两板P、Q之间的距离为d.由于金属支架运动切割磁感线,使两极板间产生的电势差为 U=Bdv
电场强度 $E=\frac{U}{d}$
由题意可知,小球进入两极板间后,所受重力与电场力相等
即 qE=mg
由以上三式可得:$q=\frac{2}{3}C$
(2)当小球进入磁场后,与金属极板之间有电场力的作用,F电=qE=mg
对金属板整个装置受力分析,地面支持力FN=Mg+F电
金属板整个装置匀速运动:F=f
摩擦力 f=μFN
由以上各式可得:F=16 N
(3)小球先做自由落体运动,$2gh={v}_{0}^{2}$
小球进入磁场后做匀速圆周运动 $q{v}_{0}^{\;}B=m\frac{{v}_{0}^{2}}{R}$
由以上两式可得 R=3 m
小球在磁场中的运动周期 $T=\frac{2πm}{qB}$
运动时间 $t=\frac{1}{2}T$
在这段时间内两极板运动的距离 x=vt=10.8 m
由题意可知,小球返回打到P板的位置到小孔的距离 l=2R+x=16.8 m
答:(1)小球所带电荷量$\frac{2}{3}C$;
(2)小球进入两极板间后,水平向右的作用力F为16N;
(3)小球返回打到P板的位置到小孔的距离16.8m.
点评 本题考查带电小球在复合场中的运动,小球受到重力、电场力和洛伦兹力作用而做匀速圆周运动必然是洛伦兹力提供向心力,重力和电场力平衡,第二问容易错,在分析金属板的受力时,必须要考虑小球对电场的反作用力,而不能认为正压力等于金属板的重力,解题时要认真分析.

 某物理兴趣小组学习了传感器的知识后,自行设计了一个氧化锡传感器用于研究用力踏油门给汽车加油时排气管中一氧化碳浓度的变化情况.实验电路图如图所示.已知踏板下面压敏电阻R1的阻值随外加压力F的增大而减小,氧化锡传感器电阻R3的倒数与一氧化碳浓度成正比,电流表和电压表均为理思电表.实验中S闭合,电键K可掷向1、2或断开.结合电路图知下列描述中正确的有( )
某物理兴趣小组学习了传感器的知识后,自行设计了一个氧化锡传感器用于研究用力踏油门给汽车加油时排气管中一氧化碳浓度的变化情况.实验电路图如图所示.已知踏板下面压敏电阻R1的阻值随外加压力F的增大而减小,氧化锡传感器电阻R3的倒数与一氧化碳浓度成正比,电流表和电压表均为理思电表.实验中S闭合,电键K可掷向1、2或断开.结合电路图知下列描述中正确的有( )| A. | K掷2时,用力踏油门则电流表的示数会减小 | |
| B. | K掷1时,增大一氧化碳浓度,则电压表的示数会增大 | |
| C. | K断开时,抬起踏板过程中,电压表的示数会减小 | |
| D. | 加入电键K是为了便于控制参量,方便研究 |
 -质量为m的实心均匀、横截面积为等边三角形的物体,沿两斜边的中点连线分别为A、B两部分,放置在光滑的支架上,支架间的距离为三角形边长的$\frac{1}{3}$,如图(a)所示;同样的等边三角形物体沿角平分线分割成C、D两部分,放置在间距为三角形边长$\frac{1}{2}$的光滑支架上,如图(b)所示,两物体均处于静止状态,则下列说法正确的是( )
-质量为m的实心均匀、横截面积为等边三角形的物体,沿两斜边的中点连线分别为A、B两部分,放置在光滑的支架上,支架间的距离为三角形边长的$\frac{1}{3}$,如图(a)所示;同样的等边三角形物体沿角平分线分割成C、D两部分,放置在间距为三角形边长$\frac{1}{2}$的光滑支架上,如图(b)所示,两物体均处于静止状态,则下列说法正确的是( )| A. | 两种情况下支架对物体的作用力相等 | |
| B. | A部分对B部分的作用力等于$\frac{1}{2}$mg | |
| C. | 支架对C部分的作用力等于mg | |
| D. | A、B两部分之间和C、D两部分之间都没有摩擦力 |
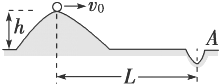 2011年8月深圳大运会高尔夫球女子团体比赛中,中华台北队获两枚金牌,中国女队队员黎佳韵在个人赛中也有不俗表现.随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图4-2-24所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直落入距击球点水平距离为L的A穴.则( )
2011年8月深圳大运会高尔夫球女子团体比赛中,中华台北队获两枚金牌,中国女队队员黎佳韵在个人赛中也有不俗表现.随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图4-2-24所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直落入距击球点水平距离为L的A穴.则( )| A. | 球被击出后做平抛运动 | |
| B. | 该球从被击出到落入A穴所用的时间为$\sqrt{\frac{2h}{g}}$ | |
| C. | 球被击出时的初速度大小为L$\sqrt{\frac{2g}{h}}$ | |
| D. | 球被击出后受到的水平风力的大小为$\frac{mgh}{L}$ |
 某同学用如图所示装置验证机械能守恒定律.通过控制电磁铁使小铁球从P点自由下落,并调整光电门Q的位置使小球下落过程中球心通过光电门中的激光束,若小铁球下落过程中经过光电门Q时,通过与之相连的毫秒计时器(图中未画出)记录下挡光时间△t,测出PQ之间的距离h,已知当地的重力加速度为g.回答下列问题:
某同学用如图所示装置验证机械能守恒定律.通过控制电磁铁使小铁球从P点自由下落,并调整光电门Q的位置使小球下落过程中球心通过光电门中的激光束,若小铁球下落过程中经过光电门Q时,通过与之相连的毫秒计时器(图中未画出)记录下挡光时间△t,测出PQ之间的距离h,已知当地的重力加速度为g.回答下列问题:
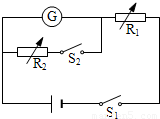 在把一个2mA电流表改装成电压表的实验中,测定电流表的内阻时,备有如下器材:
在把一个2mA电流表改装成电压表的实验中,测定电流表的内阻时,备有如下器材: