题目内容
13．长度为L=1.0m的绳，系一小球在竖直面内做圆周运动，小球的质量为m=10kg，小球半径不计，小球在通过最低点的速度大小为v=10m/s，（g取10m/s2）．试求：（1）小球在最低的向心加速度大小；
（2）小球在最低点所受绳的拉力大小．
分析 （1）根据向心加速度的公式a=$\frac{{v}^{2}}{r}$求出向心加速度的大小．
（2）在最低点靠竖直方向上的合力提供向心力，结合牛顿第二定律求出绳子对小球的拉力．
解答 解：（1）依题意有：小球在最低的向心加速度 a=$\frac{{v}^{2}}{r}=\frac{1{0}^{2}}{1}$=100m/s2，
（2）对小球在最低点受力分析有：T-mg=ma
则得 T=m（g+a）=1×（10+100）N=110N
答：（1）小球在最低的向心加速度大小为100m/s2；
（2）小球在最低点所受绳的拉力大小为110N．
点评 解决本题的关键搞清向心力的来源，根据牛顿第二定律进行求解，难度不大，属于基础题．
练习册系列答案
相关题目
3．
两个靠近的天体称为双星，它们以两者连线上某点O为圆心做匀速圆周运动，其质量分别为m1、m2，如图所示，以下说法正确的是（ ）
两个靠近的天体称为双星，它们以两者连线上某点O为圆心做匀速圆周运动，其质量分别为m1、m2，如图所示，以下说法正确的是（ ）| A． | 它们的角速度与半径成反比 | |
| B． | 它们的线速度与半径成正比 | |
| C． | 向心力与它们质量的乘积成正比 | |
| D． | 它们各自做匀速圆周运动的轨道半径与质量成反比 |
如图所示，质量分别为m和2m的A、B两物块由弹簧连接，静止在光滑的水平面上，弹簧为原长．现将质量为m，可视为质点的子弹以速度v0在极短时间内击中A并停留在其中．求：
8．
为了只用一根轻弹簧和一把刻度尺测定某滑块与水平桌面间的动摩擦因数μ（设μ为定值），设计了下述实验：第一步：如图所示，将弹簧的一端固定在竖直墙上，使滑块紧靠弹簧将其压缩，松手后滑块在水平桌面上滑行一段距离后停止；测得弹簧压缩量d与滑块向右滑行的距离s的有关数据如表所示：
根据以上数据可得出滑块滑行距离s与弹簧压缩量d间的关系应是s与d的平方成正比．
第二步：为了测出弹簧的劲度系数，将滑块挂在竖直固定的弹簧下端，弹簧伸长后保持静止状态．测得弹簧伸长量为△L，滑块质量为m，则弹簧的劲度系数k=$\frac{mg}{△L}$．
用测得的物理量d、s、△L表示滑块与桌面间的动摩擦因数μ=$\frac{{d}^{2}}{2s}$△L（弹簧弹性势能Ep=$\frac{1}{2}k{x}^{2}$，k为劲度系数，x为形变量）
为了只用一根轻弹簧和一把刻度尺测定某滑块与水平桌面间的动摩擦因数μ（设μ为定值），设计了下述实验：第一步：如图所示，将弹簧的一端固定在竖直墙上，使滑块紧靠弹簧将其压缩，松手后滑块在水平桌面上滑行一段距离后停止；测得弹簧压缩量d与滑块向右滑行的距离s的有关数据如表所示：| 试验次数 | 1 | 2 | 3 | 4 |
| d/cm | 0.50 | 1.00 | 2.00 | 4.00 |
| s/cm | 5.02 | 19.99 | 80.05 | 320.10 |
第二步：为了测出弹簧的劲度系数，将滑块挂在竖直固定的弹簧下端，弹簧伸长后保持静止状态．测得弹簧伸长量为△L，滑块质量为m，则弹簧的劲度系数k=$\frac{mg}{△L}$．
用测得的物理量d、s、△L表示滑块与桌面间的动摩擦因数μ=$\frac{{d}^{2}}{2s}$△L（弹簧弹性势能Ep=$\frac{1}{2}k{x}^{2}$，k为劲度系数，x为形变量）
18．
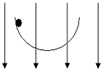一个绝缘光滑半圆环轨道放在竖直向下的匀强电场中，场强为E，在环的上端，一个质量为m，带电量为+q的小球由静止开始沿轨道运动，则（ ）
一个绝缘光滑半圆环轨道放在竖直向下的匀强电场中，场强为E，在环的上端，一个质量为m，带电量为+q的小球由静止开始沿轨道运动，则（ ）| A． | 小球运动过程中机械能守恒 | B． | 小球运动的过程中机械能减少 | ||
| C． | 在最低点球对轨道的压力为（mg+Eq） | D． | 在最低点球对轨道的压力为3（mg+Eq） |
5．一个物体处于平衡状态，下列说法不正确的是（ ）
| A． | 该物体一定静止 | B． | 该物体所受的合力一定为零 | ||
| C． | 该物体可能有很大的速度 | D． | 该物体可能受很多力 |
3．关于功率，下列说法中正确的是（ ）
| A． | 功率是用来描述物体做功多少的物理量 | |
| B． | 功率大，做的功一定多 | |
| C． | 功率小，做的功一定少 | |
| D． | 做功越快，功率越大 |