题目内容
1. 如图所示,质量分别为m和2m的A、B两物块由弹簧连接,静止在光滑的水平面上,弹簧为原长.现将质量为m,可视为质点的子弹以速度v0在极短时间内击中A并停留在其中.求:
如图所示,质量分别为m和2m的A、B两物块由弹簧连接,静止在光滑的水平面上,弹簧为原长.现将质量为m,可视为质点的子弹以速度v0在极短时间内击中A并停留在其中.求:(1)最大的弹性势能
(2)物块B的最大速度.
分析 (1)子弹射入物块A后,A获得速度将压缩弹簧,B受到弹力作用而加速,A做减速运动,当两者速度相同时弹簧的压缩量最大,弹性势能最大.先根据动量守恒定律求出子弹射入A后两者的共同速度.再由动量守恒定律求三者共同速度,由能量守恒定律可以求出弹簧的最大弹性势能.
(2)当弹簧恢复原长时,B的速度最大,由动量守恒定律和能量守恒定律结合可以求出B的最大速度.
解答 解:(1)子弹击中A的过程,子弹与A组成的系统动量守恒,以子弹的初速度方向为正方向,由动量守恒定律得:
mv0=(m+m)v1,解得 v1=0.5v0.
当A、B速度相等时,弹簧的弹性势能最大,以子弹、A、B组成的系统为研究对象,
以A的初速度方向为正方向,由动量守恒定律得:
(m+m)v1=(m+m+2m)v2,
由能量守恒定律得:
$\frac{1}{2}$(m+m)v12=EP+$\frac{1}{2}$(m+m+2m)v22,
解得:EP=$\frac{1}{8}m{v}_{0}^{2}$
(2)当弹簧被压缩到最短再次回复原长时,B的速度最大,设此时A、B的速度分别为vA和vB.
由动量守恒定律得:
2mv1=2mvA+2mvB;
由机械能守恒定律得:
$\frac{1}{2}$×2mv12=$\frac{1}{2}$×2mvA2+$\frac{1}{2}$×2mvB2;
解得:vB=v1=0.5v0.
答:
(1)最大的弹性势能是$\frac{1}{8}m{v}_{0}^{2}$.
(2)物块B的最大速度是0.5v0.
点评 本题考查了求弹性势能、求速度,分析清楚运动过程是正确解题的关键,应用动量守恒定律与能量守恒定律即可正确解题.要注意子弹射入A中的过程,有机械能损失,不能全过程运用机械能守恒定律列式.

练习册系列答案
相关题目
11.两个质点之间万有引力的大小为F,如果只将这两个质点之间的距离变为原来的2倍,其他条件不变,那么它们之间万有引力的大小变为( )
| A. | $\frac{F}{4}$ | B. | $\frac{F}{2}$ | C. | 2F | D. | 4F |
12. 在圆轨道上运动的国际空间站里,一宇航员A静止(相对空间舱)“站”于舱内朝向地球一侧的“地面”B上,如图所示,下列说法正确的是( )
在圆轨道上运动的国际空间站里,一宇航员A静止(相对空间舱)“站”于舱内朝向地球一侧的“地面”B上,如图所示,下列说法正确的是( )
 在圆轨道上运动的国际空间站里,一宇航员A静止(相对空间舱)“站”于舱内朝向地球一侧的“地面”B上,如图所示,下列说法正确的是( )
在圆轨道上运动的国际空间站里,一宇航员A静止(相对空间舱)“站”于舱内朝向地球一侧的“地面”B上,如图所示,下列说法正确的是( )| A. | 宇航员不受地球引力作用 | |
| B. | 宇航员受到地球的引力和空间站“地面”对他的支持力 | |
| C. | 宇航员与空间站“地面”之间无相互作用力,因为宇航员处于完全失重状态 | |
| D. | 若宇航员将手中一小球无初速度(相对空间舱)释放,该小球将落到空间站“地面”上 |
9.下列说法中正确的是( )
| A. | 全息照相的拍摄利用了光的干涉原理 | |
| B. | 拍摄玻璃厨窗内的物品时,往往在镜头前加一个偏振片以增加透射光的强度 | |
| C. | 真空中的光速在不同的惯性参考系中都是相同的,与光源和观察者的运动无关 | |
| D. | 医学上用激光做“光刀”来进行手术,主要是利用了激光的亮度高、能量大的特点 |
16.下面是金星、地球、火星的有关情况比较.
根据以上信息,关于地球及地球的两个邻居金星和火星(行星的运动可看作圆周运动),下列判断正确的是( )
| 星球 | 金星 | 地球 | 火星 |
| 公转半径 | 1.0×108 km | 1.5×108 km | 2.25×108km |
| 自转周期 | 243日 | 23时56分 | 24时37分 |
| 表面温度 | 480℃ | 15℃ | -100℃~0℃ |
| 大气主要成分 | 约95%的CO2 | 78%的N2,21%的O2 | 约95%的CO2 |
| A. | 金星运行的线速度最小,火星运行的线速度最大 | |
| B. | 金星公转的向心加速度大于地球公转的向心加速度 | |
| C. | 金星的公转周期一定比地球的公转周期小 | |
| D. | 金星运行的角速度最小,火星运动的角速度最大 |
6.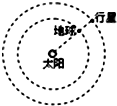 某行星和地球绕太阳公转的轨道均可视为圆,每过N年,该行星会运行到日地连线的延长线上,如图所示,该行星与地球的公转半径比为( )
某行星和地球绕太阳公转的轨道均可视为圆,每过N年,该行星会运行到日地连线的延长线上,如图所示,该行星与地球的公转半径比为( )
 某行星和地球绕太阳公转的轨道均可视为圆,每过N年,该行星会运行到日地连线的延长线上,如图所示,该行星与地球的公转半径比为( )
某行星和地球绕太阳公转的轨道均可视为圆,每过N年,该行星会运行到日地连线的延长线上,如图所示,该行星与地球的公转半径比为( )| A. | ($\frac{N}{N-1}$)${\;}^{\frac{2}{3}}$ | B. | ($\frac{N+1}{N}$)${\;}^{\frac{3}{2}}$ | C. | ($\frac{N}{N-1}$)${\;}^{\frac{3}{2}}$ | D. | ($\frac{N+1}{N}$)${\;}^{\frac{2}{3}}$ |
10.下列说法正确的是( )
| A. | 可利用某些物质在紫外线照射下发出荧光来设计防伪措施 | |
| B. | 根据多普勒效应可以判断遥远天体相对于地球的运动速度 | |
| C. | 光波和无线电波同属电磁波,光波的频率比无线电波的频率低,波长比无线电波的波长大,在真空中传播的速度都约为3.0×108 m/s | |
| D. | “和谐号”动车组高速行驶时,在地面上测得的其车厢长度略微变短 |
11.下列说法中正确的是( )
| A. | 物体的速度越大,加速度一定越大 | |
| B. | 物体的速度变化得越快,加速度越大 | |
| C. | 物体的加速度不断减小,速度一定越来越小 | |
| D. | 物体在某时刻的速度为零,其加速度也一定为零 |