题目内容
16.火星跟地球的相似度很高,被认为是人类进行星际移民的首选之地.将火星和地球绕太阳的运动视为匀速圆周运动,已知火星与地球的质量之比为p、轨道半径之比为q,则火星与地球绕太阳运动的角速度大小之比为( )| A. | $\frac{p}{q}$ | B. | $\frac{q}{p}$ | C. | $\frac{1}{q}$ | D. | $\frac{1}{{q}^{\frac{3}{2}}}$ |
分析 由万有引力提供向心力可以列出关于角速度的表达式,再求得比值.
解答 解:根据万有引力提供向心力,有:
$G\frac{Mm}{{r}_{\;}^{2}}=m{ω}_{\;}^{2}r$
解得:$ω=\sqrt{\frac{GM}{{r}_{\;}^{3}}}$
所以火星与地球绕太阳运动的角速度大小之比为:
$\frac{{ω}_{1}^{\;}}{{ω}_{2}^{\;}}=\sqrt{\frac{{r}_{2}^{3}}{{r}_{1}^{3}}}$=$\sqrt{\frac{1}{{q}_{\;}^{3}}}$=$\frac{1}{{q}^{\frac{3}{2}}}$,故D正确,ABC错误;
故选:D
点评 求一个物理量之比,我们应该把这个物理量先用已知的物理量表示出来,再根据表达式进行比较.向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
9. 如图所示,足够长的水平传送带以恒定速率v运动,现将质量均为m的甲、乙两小物体先后轻放在传送带的最左端,两物体速率达到v时通过的位移分别为S甲、S乙,且S甲>S乙,则在两物体加速运动过程中,下列说法正确的是( )
如图所示,足够长的水平传送带以恒定速率v运动,现将质量均为m的甲、乙两小物体先后轻放在传送带的最左端,两物体速率达到v时通过的位移分别为S甲、S乙,且S甲>S乙,则在两物体加速运动过程中,下列说法正确的是( )
 如图所示,足够长的水平传送带以恒定速率v运动,现将质量均为m的甲、乙两小物体先后轻放在传送带的最左端,两物体速率达到v时通过的位移分别为S甲、S乙,且S甲>S乙,则在两物体加速运动过程中,下列说法正确的是( )
如图所示,足够长的水平传送带以恒定速率v运动,现将质量均为m的甲、乙两小物体先后轻放在传送带的最左端,两物体速率达到v时通过的位移分别为S甲、S乙,且S甲>S乙,则在两物体加速运动过程中,下列说法正确的是( )| A. | 传送带对两物体做的功相等 | |
| B. | 两物体加速运动的时间相等 | |
| C. | 两物体加速运动的加速度相等 | |
| D. | 两过程中摩擦力对传送带做的功相等 |
11. 真空中有一竖直向上的匀强电场,其场强大小为E,电场中的A、B两点固定着两个等量异号点电荷+Q、-Q,A、B两点的连线水平,O为其连线的中点,c、d是两点电荷连线垂直平分钱上的两点,Oc=Od,a、b两点在两点电荷的连线上,且Oa=Ob.下列判断正确的是( )
真空中有一竖直向上的匀强电场,其场强大小为E,电场中的A、B两点固定着两个等量异号点电荷+Q、-Q,A、B两点的连线水平,O为其连线的中点,c、d是两点电荷连线垂直平分钱上的两点,Oc=Od,a、b两点在两点电荷的连线上,且Oa=Ob.下列判断正确的是( )
 真空中有一竖直向上的匀强电场,其场强大小为E,电场中的A、B两点固定着两个等量异号点电荷+Q、-Q,A、B两点的连线水平,O为其连线的中点,c、d是两点电荷连线垂直平分钱上的两点,Oc=Od,a、b两点在两点电荷的连线上,且Oa=Ob.下列判断正确的是( )
真空中有一竖直向上的匀强电场,其场强大小为E,电场中的A、B两点固定着两个等量异号点电荷+Q、-Q,A、B两点的连线水平,O为其连线的中点,c、d是两点电荷连线垂直平分钱上的两点,Oc=Od,a、b两点在两点电荷的连线上,且Oa=Ob.下列判断正确的是( )| A. | a、b两点的电场强度相同 | |
| B. | c点的电势比d点的电势低 | |
| C. | 将电子从a点移到c点的过程中,电场力对电子做负功 | |
| D. | 将电子从a点移到b点时其电势能减小 |
1.斯诺克比赛中,一枚质量为m的红球桌面上滚动.下列判断正确的是( )
| A. | 滚动的红球只受到重力 | |
| B. | 物体所受重力可以用G=mg计算 | |
| C. | 如果桌面不水平.红球所受重力与桌面垂直 | |
| D. | 只有红球的中心部位受到重力作用 |
8. 一个静止的放射性同位素的原子核${\;}_{15}^{30}$P衰变为${\;}_{14}^{30}$Si,另一个静止的天然放射性元素的原子核${\;}_{90}^{234}$Th衰变为${\;}_{91}^{234}$Pa,在同一磁场中,得到衰变后粒子的运动径迹1、2、3、4,如图所示,则这四条径迹依次是( )
一个静止的放射性同位素的原子核${\;}_{15}^{30}$P衰变为${\;}_{14}^{30}$Si,另一个静止的天然放射性元素的原子核${\;}_{90}^{234}$Th衰变为${\;}_{91}^{234}$Pa,在同一磁场中,得到衰变后粒子的运动径迹1、2、3、4,如图所示,则这四条径迹依次是( )
 一个静止的放射性同位素的原子核${\;}_{15}^{30}$P衰变为${\;}_{14}^{30}$Si,另一个静止的天然放射性元素的原子核${\;}_{90}^{234}$Th衰变为${\;}_{91}^{234}$Pa,在同一磁场中,得到衰变后粒子的运动径迹1、2、3、4,如图所示,则这四条径迹依次是( )
一个静止的放射性同位素的原子核${\;}_{15}^{30}$P衰变为${\;}_{14}^{30}$Si,另一个静止的天然放射性元素的原子核${\;}_{90}^{234}$Th衰变为${\;}_{91}^{234}$Pa,在同一磁场中,得到衰变后粒子的运动径迹1、2、3、4,如图所示,则这四条径迹依次是( )| A. | 图中1、2为${\;}_{90}^{234}$Th衰变产生的${\;}_{91}^{234}$Pa和${\;}_{-1}^{0}$e的轨迹,其中1是电子${\;}_{-1}^{0}$e的轨迹 | |
| B. | 图中1、2为${\;}_{15}^{30}$P衰变产生的${\;}_{14}^{30}$Si和${\;}_{1}^{0}$e的轨迹,其中2是正电子${\;}_{1}^{0}$e的轨迹 | |
| C. | 图中3、4是${\;}_{15}^{30}$P衰变产生的${\;}_{14}^{30}$Si和${\;}_{1}^{0}$e的轨迹,其中3是正电子${\;}_{1}^{0}$e的轨迹 | |
| D. | 图中3、4轨迹中两粒子在磁场中旋转方向相反 |
5.有关欧姆表的使用,下列说法中正确的是( )
| A. | 测量电阻时,表的指针偏转角度越大,误差就越小 | |
| B. | 更换测量挡时,需要重新调零 | |
| C. | 使用完毕应将选择开关旋至交流电压最高挡或“OFF”挡 | |
| D. | 欧姆表如果用×100Ω挡指针相对电流零刻度偏转太小,应改用×1kΩ挡或更高挡测量 |


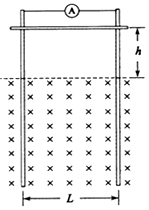 如图所示,两根足够长的光滑金属导轨竖直放置,相距为L,一理想电流表与两导轨相连,匀强磁场与导轨平面垂直.磁感应强度为B,一质量为m、有效电阻为R的导体棒在距磁场上边界h处静止释放.导体棒进入磁场后,流经电流表的电流逐渐减小,最终稳定.整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻.求:
如图所示,两根足够长的光滑金属导轨竖直放置,相距为L,一理想电流表与两导轨相连,匀强磁场与导轨平面垂直.磁感应强度为B,一质量为m、有效电阻为R的导体棒在距磁场上边界h处静止释放.导体棒进入磁场后,流经电流表的电流逐渐减小,最终稳定.整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻.求: