题目内容
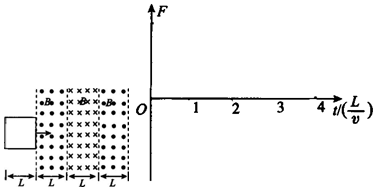
8. 一个静止的放射性同位素的原子核${\;}_{15}^{30}$P衰变为${\;}_{14}^{30}$Si,另一个静止的天然放射性元素的原子核${\;}_{90}^{234}$Th衰变为${\;}_{91}^{234}$Pa,在同一磁场中,得到衰变后粒子的运动径迹1、2、3、4,如图所示,则这四条径迹依次是( )
一个静止的放射性同位素的原子核${\;}_{15}^{30}$P衰变为${\;}_{14}^{30}$Si,另一个静止的天然放射性元素的原子核${\;}_{90}^{234}$Th衰变为${\;}_{91}^{234}$Pa,在同一磁场中,得到衰变后粒子的运动径迹1、2、3、4,如图所示,则这四条径迹依次是( )| A. | 图中1、2为${\;}_{90}^{234}$Th衰变产生的${\;}_{91}^{234}$Pa和${\;}_{-1}^{0}$e的轨迹,其中1是电子${\;}_{-1}^{0}$e的轨迹 | |
| B. | 图中1、2为${\;}_{15}^{30}$P衰变产生的${\;}_{14}^{30}$Si和${\;}_{1}^{0}$e的轨迹,其中2是正电子${\;}_{1}^{0}$e的轨迹 | |
| C. | 图中3、4是${\;}_{15}^{30}$P衰变产生的${\;}_{14}^{30}$Si和${\;}_{1}^{0}$e的轨迹,其中3是正电子${\;}_{1}^{0}$e的轨迹 | |
| D. | 图中3、4轨迹中两粒子在磁场中旋转方向相反 |
分析 放射性元素的原子核,沿垂直于磁场方向放射出一个粒子后进入匀强磁场,在洛伦兹力的作用下都做匀速圆周运动.放射性元素放出粒子,动量守恒,由半径公式r=$\frac{mv}{Bq}$=$\frac{P}{Bq}$,分析α粒子和β粒子与反冲核半径关系,根据洛伦兹力分析运动轨迹是内切圆还是外切圆,判断是哪种衰变.
解答 解:放射性元素放出正电子时,正粒子与反冲核的速度方向相反,而电性相同,则两个粒子受到的洛伦兹力方向相反,两个粒子的轨迹应为外切圆.
而放射性元素放出β粒子时,β粒子与反冲核的速度方向相反,而电性相反,则两个粒子受到的洛伦兹力方向相同,两个粒子的轨迹应为内切圆.
放射性元素放出粒子时,两带电粒子的动量守恒.由半径公式r=$\frac{mv}{Bq}$=$\frac{P}{Bq}$,可得轨迹半径与动量成正比,与电量成反比,而正电子和β粒子的电量比反冲核的电量小,则正电子和β粒子的半径比反冲核的半径都大,故轨迹1、2、3、4依次是:${\;}_{91}^{234}$Pa、电子、正电子、${\;}_{14}^{30}$Si;
由上分析,可知,故C正确,ABD错误.
故选:C.
点评 放射性元素放射后,两带电粒子的动量是守恒.正好轨迹的半径公式中也有动量的大小,所以可以研究半径与电荷数的关系.

练习册系列答案
相关题目
1. 半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两小球分别自半圆形槽左边缘的最高点无初速度地释放,在下滑过程中( )
半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两小球分别自半圆形槽左边缘的最高点无初速度地释放,在下滑过程中( )
 半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两小球分别自半圆形槽左边缘的最高点无初速度地释放,在下滑过程中( )
半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两小球分别自半圆形槽左边缘的最高点无初速度地释放,在下滑过程中( )| A. | 两小球机械能均逐渐减小 | B. | 两小球机械能总是相等的 | ||
| C. | 两小球经最低点时动能相等 | D. | 两小球到最低点时重力做功相等 |
16.火星跟地球的相似度很高,被认为是人类进行星际移民的首选之地.将火星和地球绕太阳的运动视为匀速圆周运动,已知火星与地球的质量之比为p、轨道半径之比为q,则火星与地球绕太阳运动的角速度大小之比为( )
| A. | $\frac{p}{q}$ | B. | $\frac{q}{p}$ | C. | $\frac{1}{q}$ | D. | $\frac{1}{{q}^{\frac{3}{2}}}$ |
3. 竖直放置的平行光滑导轨,其电阻不计,磁场方向如图所示,磁感强度B=1T,重为G1=0.5N的导体棒ab及重为G2=0.4N的导体棒cd长均为0.5m,电阻均为1Ω,现要使其中一棒静止不动,另一棒做匀速运动(不计一切摩擦,两棒与导轨始终接触良好),下列说法正确的是( )
竖直放置的平行光滑导轨,其电阻不计,磁场方向如图所示,磁感强度B=1T,重为G1=0.5N的导体棒ab及重为G2=0.4N的导体棒cd长均为0.5m,电阻均为1Ω,现要使其中一棒静止不动,另一棒做匀速运动(不计一切摩擦,两棒与导轨始终接触良好),下列说法正确的是( )
 竖直放置的平行光滑导轨,其电阻不计,磁场方向如图所示,磁感强度B=1T,重为G1=0.5N的导体棒ab及重为G2=0.4N的导体棒cd长均为0.5m,电阻均为1Ω,现要使其中一棒静止不动,另一棒做匀速运动(不计一切摩擦,两棒与导轨始终接触良好),下列说法正确的是( )
竖直放置的平行光滑导轨,其电阻不计,磁场方向如图所示,磁感强度B=1T,重为G1=0.5N的导体棒ab及重为G2=0.4N的导体棒cd长均为0.5m,电阻均为1Ω,现要使其中一棒静止不动,另一棒做匀速运动(不计一切摩擦,两棒与导轨始终接触良好),下列说法正确的是( )| A. | 要使ab棒静止不动,cd棒向下匀速运动的速度大小是3.2 m/s | |
| B. | 要使ab棒静止不动,cd受到竖直向上的推力大小是0.9 N | |
| C. | 要使cd棒静止不动,ab棒向上匀速运动的速度大小是4 m/s | |
| D. | 要使cd棒静止不动,ab受到竖直向上的推力大小是0.9 N |
20.对开普勒第三定律$\frac{{a}^{3}}{{T}^{2}}$=k,以下理解正确的是( )
| A. | a代表行星运动的轨道半径 | B. | k是一个与行星有关的常量 | ||
| C. | T代表行星运动的自转周期 | D. | T代表行星运动的公转周期 |
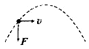
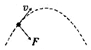
9. 一质量为m的小球,用长为L的轻绳悬挂于O点.小球在水平力F作用下,从平衡位置P点移动到Q点,如图所示,关于力F所做的功下列说法正确的是( )
一质量为m的小球,用长为L的轻绳悬挂于O点.小球在水平力F作用下,从平衡位置P点移动到Q点,如图所示,关于力F所做的功下列说法正确的是( )
 一质量为m的小球,用长为L的轻绳悬挂于O点.小球在水平力F作用下,从平衡位置P点移动到Q点,如图所示,关于力F所做的功下列说法正确的是( )
一质量为m的小球,用长为L的轻绳悬挂于O点.小球在水平力F作用下,从平衡位置P点移动到Q点,如图所示,关于力F所做的功下列说法正确的是( )| A. | 若水平力F是恒定的力,则力F所做的功为FLsinθ | |
| B. | 若水平力F是恒定的力,则力F所做的功为FL(1-cosθ) | |
| C. | 若是把小球缓慢移动,则力F所做的功为mgL(1-cosθ) | |
| D. | 若是把小球缓慢移动,则力F所做的功为FLsinθ |