题目内容
20. 如图所示,平行放置的金属板A、B间电压为U0,中心各有一个小孔P、Q,平行放置的金属板C、D板长和板间距均为L,足够长的粒子接收屏M与D板夹角为127°.现从P点处有质量为 m、带电量为+q的粒子放出(粒子的初速度可忽略不计).经加速后从Q点射出,贴着C板并平行C板射入C、D电场(平行金属板外电场忽略不计,重力不计,sin3°=0.6,cos37°=0.8)
如图所示,平行放置的金属板A、B间电压为U0,中心各有一个小孔P、Q,平行放置的金属板C、D板长和板间距均为L,足够长的粒子接收屏M与D板夹角为127°.现从P点处有质量为 m、带电量为+q的粒子放出(粒子的初速度可忽略不计).经加速后从Q点射出,贴着C板并平行C板射入C、D电场(平行金属板外电场忽略不计,重力不计,sin3°=0.6,cos37°=0.8)(1)粒子经加速后从Q点射出速度大小v.
(2)若在进入C、D间电场后好恰从D板边缘飞出,则C、D间电压U1为多少?
(3)调节C、D间电压(大小)使进入电场的粒子,不能打在粒子接收屏M上,则C、D间电压U2的取值范围?
分析 (1)先由动能定理求出电场加速获得的速度.
(2)若在t=0时刻进入C、D间电场的粒子恰从D板边缘飞出,粒子在CD间先做类平抛运动,后沿速度方向做匀速直线运动,根据牛顿第二定律和运动学公式结合求解.
(3)不能打在粒子接收屏M上的粒子,可能落在极板D上,有可能飞出电场时的偏转角比较小,由类平抛运动的公式分别讨论即可.
解答 解:(1)在AB之间电场力做功,由动能定理:$\frac{1}{2}mv_{\;}^2-0=q{U_0}$
所以:$v=\sqrt{\frac{{2q{U_0}}}{m}}$
(2)粒子在偏转电场中水平方向做匀速直线运动得:$t=\frac{L}{v}=L\sqrt{\frac{m}{2q{U}_{0}}}$
竖直方向上做匀加速直线运动$a=\frac{{q{U_1}}}{mL}$
竖直方向上位移$L=\frac{1}{2}\frac{{q{U_1}}}{mL}{t^2}$
求得U1=4U0
(3)若粒子飞出C、D间电场则飞出时竖直方向上速度${v_y}=\frac{{q{U_1}}}{mv}\sqrt{\frac{m}{2qU}}$
速度偏转角$tanθ=\frac{v_y}{v_x}=\frac{U_2}{{2{U_1}}}$
由题意可知θ≤53°解得${U_2}≤\frac{{3{U_1}}}{2}$
若粒子没有飞出电场也不能打到粒子接收屏M;此时可知U1>4U0
综上:可知U1>4U0或 ${U_2}≤\frac{{3{U_1}}}{2}$
答:(1)粒子经加速后从Q点射出速度大小是$\sqrt{\frac{2q{U}_{0}}{m}}$.
(2)若在进入C、D间电场后好恰从D板边缘飞出,则C、D间电压U1为4U0;
(3)调节C、D间电压(大小)使进入电场的粒子,不能打在粒子接收屏M上,则C、D间电压U2的取值范围U1>4U0或 ${U_2}≤\frac{{3{U_1}}}{2}$.
点评 本题关键是分析带电粒子的运动情况,确定出临界条件,运用牛顿第二定律和运动学规律结合进行求解.

| A. | 物体通过一段路程,则它通过的位移不可能为零 | |
| B. | 物体沿直线运动,通过的路程一定等于位移大小 | |
| C. | 物体两次通过的路程不等,位移不可能相等 | |
| D. | 路程是标量,只有大小;位移是矢量,有大小也有方向 |

| A. | 两物体相遇的时间是2s和6s | |
| B. | 乙物体先向前运动2s,随后向后运动 | |
| C. | 两个物体相距最远的时刻是4s末 | |
| D. | 4s后甲在乙前面 |
 如图所示,虚线框中存在垂直纸面向外的匀强磁场B和平行纸面且与竖直平面夹角为45°斜向下的匀强电场E,有一质量为m,电荷量为q的带负电的小球在高为h处的P点从静止开始自由下落,当小球运动到复合场内时刚好做直线运动,那么( )
如图所示,虚线框中存在垂直纸面向外的匀强磁场B和平行纸面且与竖直平面夹角为45°斜向下的匀强电场E,有一质量为m,电荷量为q的带负电的小球在高为h处的P点从静止开始自由下落,当小球运动到复合场内时刚好做直线运动,那么( )| A. | 小球在复合场中一定做匀速直线运动 | |
| B. | 磁感应强度B=$\frac{{m\sqrt{2gh}}}{2qh}$,场强E=$\frac{{\sqrt{2}mg}}{q}$ | |
| C. | 若换成带正电的小球,小球仍可能做直线运动 | |
| D. | 若同时改变小球比荷及初始下落高度h,小球仍能沿直线通过复合场 |
| A. | 200 W | B. | 100 W | C. | 50 W | D. | 25 W |
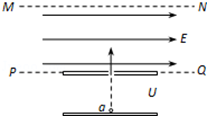 如图所示,虚线PQ、MN间存在水平匀强电场,一带电粒子质量为m=2.0×10-11kg、电荷量为q=+1.0×10-5C,从a点由静止开始经电压为U=100V的电场加速后,垂直于匀强电场进入匀强电场中,从虚线MN的某点b(图中未画出)离开匀强电场时速度与电场方向成30°角.已知PQ、MN间距为20cm,带电粒子的重力忽略不计.求:
如图所示,虚线PQ、MN间存在水平匀强电场,一带电粒子质量为m=2.0×10-11kg、电荷量为q=+1.0×10-5C,从a点由静止开始经电压为U=100V的电场加速后,垂直于匀强电场进入匀强电场中,从虚线MN的某点b(图中未画出)离开匀强电场时速度与电场方向成30°角.已知PQ、MN间距为20cm,带电粒子的重力忽略不计.求:
 如图所示,匀强电场电场线与AC平行,AB与AC成60°角,把10-8C的负电荷A移到B,电场力做功6×10-8J,AB间距离6cm,则场强方向为与CA平行且向下,如B处电势为1V,则A处为-5V,电子在A点的电势能为5eV.
如图所示,匀强电场电场线与AC平行,AB与AC成60°角,把10-8C的负电荷A移到B,电场力做功6×10-8J,AB间距离6cm,则场强方向为与CA平行且向下,如B处电势为1V,则A处为-5V,电子在A点的电势能为5eV. 如图,平行板间电压为U,板间距离为d,板长为L1,一带电粒子质量为m,电荷量为q,以初速度v0垂直于场强方向射入电场中,离开电场中沿直线打在光屏上,光屏到平行板近端的距离为L2,不计粒子重力.求
如图,平行板间电压为U,板间距离为d,板长为L1,一带电粒子质量为m,电荷量为q,以初速度v0垂直于场强方向射入电场中,离开电场中沿直线打在光屏上,光屏到平行板近端的距离为L2,不计粒子重力.求