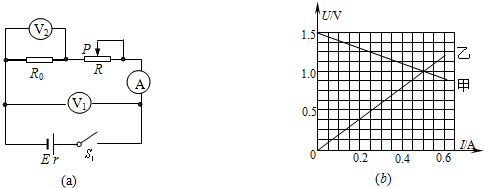题目内容
20.双星系统是由两个星体构成,其中每个星体的线度都小于两星体间的距离,一般双星系统距离其它星体很远,可以当做孤立系统处理,现根据对某一双星系统的光度学测量确定,该双星系统中每个星体的质量都是M,两者相距L,它们正围绕两者连线的中点做圆周运动. 计算该双星系统的运动周期T计算.分析 根据万有引力提供向心力,每个星体的质量都是M,两者相距L,所以每一个的轨道半径都是$\frac{1}{2}$L,由$\frac{GMM}{{L}^{2}}=\frac{M•4{π}^{2}r}{{T}^{2}}$即可求出双星系统的运动周期.
解答 解:根据万有引力提供向心力得,$\frac{GMM}{{L}^{2}}=M(\frac{2π}{{T}_{计算}})^{2}•\frac{L}{2}$,
解得${T}_{计算}=2π\sqrt{\frac{{L}^{3}}{2GM}}$.
答:该双星系统的运动周期是$2π\sqrt{\frac{{L}^{3}}{2GM}}$.
点评 本题关键找出向心力来源,然后根据牛顿第二定律列方程求解,要细心,不难.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
10.如图1,用频率为ν的光照射光电管内的金属材料B,发生光电效应,调节滑片P,当电流计G的示数为零时记下电压表V的示数(U表示)然后更换频率不同的光重复上述实验过程,可测出一组ν-U数据,作图如图2所示,甲、乙表示两种不同的金属.有关说法正确的是( )
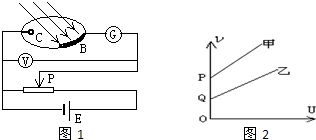

| A. | 金属甲的逸出功大于乙的 | |
| B. | 甲、乙两条直线一定是平行的(图中画的是不平行的) | |
| C. | 金属甲的逸出功小于乙的 | |
| D. | 甲、乙两条直线一定是不平行的 |
8.关于合运动与分运动,下列说法正确的是( )
| A. | 合运动与分运动体现了等效替代的思想 | |
| B. | 合运动与分运动具有等时性的特点 | |
| C. | 分运动都是匀速直线运动,它们的合运动可能是匀变速直线运动 | |
| D. | 同一物体的各分运动可能相互影响 |
15.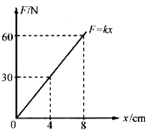 一根弹簧的弹力-位移图线如图所示,那么弹簧由伸长量8cm变到伸长量4cm的过程中,弹力所做的功和弹性势能的变化量为( )
一根弹簧的弹力-位移图线如图所示,那么弹簧由伸长量8cm变到伸长量4cm的过程中,弹力所做的功和弹性势能的变化量为( )
 一根弹簧的弹力-位移图线如图所示,那么弹簧由伸长量8cm变到伸长量4cm的过程中,弹力所做的功和弹性势能的变化量为( )
一根弹簧的弹力-位移图线如图所示,那么弹簧由伸长量8cm变到伸长量4cm的过程中,弹力所做的功和弹性势能的变化量为( )| A. | 3.6J,-3.6J | B. | -3.6J,3.6J | C. | 1.8J,-1.8J | D. | -1.8J,1.8J |
5.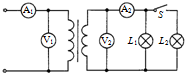 如图所示,理想变压器原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,交流电压表V1、V2和电流表A1、A2均为理想电表,导线电阻不计.当开关S闭合后( )
如图所示,理想变压器原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,交流电压表V1、V2和电流表A1、A2均为理想电表,导线电阻不计.当开关S闭合后( )
 如图所示,理想变压器原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,交流电压表V1、V2和电流表A1、A2均为理想电表,导线电阻不计.当开关S闭合后( )
如图所示,理想变压器原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,交流电压表V1、V2和电流表A1、A2均为理想电表,导线电阻不计.当开关S闭合后( )| A. | A1示数变大,A1与A2示数的比值变大 | |
| B. | A1示数变大,A1与A2示数的比值不变 | |
| C. | V2示数变小,V1与V2示数的比值变大 | |
| D. | V2示数不变,V1与V2示数的比值不变 |
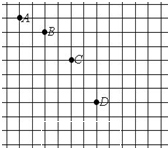 如图,在“研究平抛物体的运动”的实验中,用一张印有小格子的纸记录轨迹,小方格的边长L=1.25cm,若小球在运动途中的几个位置如图中的A、B、C、D所示,则
如图,在“研究平抛物体的运动”的实验中,用一张印有小格子的纸记录轨迹,小方格的边长L=1.25cm,若小球在运动途中的几个位置如图中的A、B、C、D所示,则