题目内容
7. 虚线MN为足够大的光滑水平面上的一条界线,界线的右侧是力的作用区.OP为力的作用区内一条直线,OP与界线MN夹角为α.可视为质点的不同小球,沿光滑水平面从界线的O点不断地射入力的作用区内,小球一进入力的作用区就受到水平恒力作用,水平恒力方向平行于MN且由M指向N,恒力大小与小球的重力成正比,比例系数为k N/kg,试求:
虚线MN为足够大的光滑水平面上的一条界线,界线的右侧是力的作用区.OP为力的作用区内一条直线,OP与界线MN夹角为α.可视为质点的不同小球,沿光滑水平面从界线的O点不断地射入力的作用区内,小球一进入力的作用区就受到水平恒力作用,水平恒力方向平行于MN且由M指向N,恒力大小与小球的重力成正比,比例系数为k N/kg,试求:(1)当小球速度为v0,射入方向与界线MN的夹角为β时,小球在力的作用区内的最小速度的大小;
(2)当小球以速度v0垂直界线MN射入时,小球从开始射入到(未越过OP直线),距离OP直线最远处所经过的时间;(说明:OP方向为右上方,v0与MN的夹角为β是的方向为右下方)
分析 (1)将小球的运动分解为平行于MN方向和垂直于MN方向,当平行于MN方向的速度为零时,小球的速度最小.
(2)当小球的速度方向与0P平行时,距离OP直线最远.根据沿MN方向和垂直于MN方向上的运动规律得出两个分速度,结合平行四边形定则求出沿MN方向上的分速度的大小根据速度时间公式求出运动的时间.
解答 解:(1)由题意分析可知,当小球平行于MN方向的速度为零时,此时速度最小,根据平行四边形定则知,vmin=v0sinβ
(2)由F=kmg得:a=$\frac{F}{mg}$=k
垂直MN方向上,vx=v0,
沿MN方向上vy=at=kgt
当小球的速度方向与0P平行时,距离OP直线最远.
则vy=v0cotα
解得t=$\frac{{v}_{0}cotα}{kg}$ 
答:(1)当小球速度为v0,射入方向与界线MN的夹角为β时,小球在力的作用区内的最小速度的大小v0sinβ;
(2)距离OP直线最远处所经过的时间$\frac{{v}_{0}cotα}{kg}$.
点评 解决本题的关键对小球的运动进行分解,结合分运动规律,抓住等时性,根据牛顿第二定律和运动学公式综合求解.

练习册系列答案
相关题目
15.在太阳系中有一颗行星的半径为R,若在该星球表面以初速度v0竖直上抛出一物体,该物体上升的最大高度为H.已知该物体所受的其他力与行星对它的万有引力相比较可忽略不计.则根据这些条件,不可以求出的物理量是( )
| A. | 该行星的密度 | B. | 该行星的自转周期 | ||
| C. | 该星球的第一宇宙速度 | D. | 该行星附近运行的卫星的最小周期 |
2. 如图所示,用两根绝缘丝线挂着两个质量相同、均不带电的小球A和B,此时,上、下丝线的张力分别为FA、FB;如果使A带正电,B带负电,此时上、下丝线的张力分别为FA′、FB′,则有( )
如图所示,用两根绝缘丝线挂着两个质量相同、均不带电的小球A和B,此时,上、下丝线的张力分别为FA、FB;如果使A带正电,B带负电,此时上、下丝线的张力分别为FA′、FB′,则有( )
 如图所示,用两根绝缘丝线挂着两个质量相同、均不带电的小球A和B,此时,上、下丝线的张力分别为FA、FB;如果使A带正电,B带负电,此时上、下丝线的张力分别为FA′、FB′,则有( )
如图所示,用两根绝缘丝线挂着两个质量相同、均不带电的小球A和B,此时,上、下丝线的张力分别为FA、FB;如果使A带正电,B带负电,此时上、下丝线的张力分别为FA′、FB′,则有( )| A. | FA<FA′ | B. | FA=FA′ | C. | FB>FB′ | D. | FB<FB′ |
12.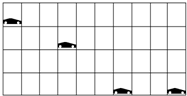 做杂技表演的汽车从高台水平飞出,在空中运动后着地,一架照相机通过多次曝光,拍摄得到汽车在着地前后一段时间内的运动照片,并且汽车刚好到达地面时拍到一次.如图所示,已知汽车长度为3.6m,相邻两次曝光时间间隔相等,由照片(图中实线是用笔画的正方形的格子)可推算出汽车离开高台时的瞬时速度大小和高台离地面高度分别为(g取10m/s2)( )
做杂技表演的汽车从高台水平飞出,在空中运动后着地,一架照相机通过多次曝光,拍摄得到汽车在着地前后一段时间内的运动照片,并且汽车刚好到达地面时拍到一次.如图所示,已知汽车长度为3.6m,相邻两次曝光时间间隔相等,由照片(图中实线是用笔画的正方形的格子)可推算出汽车离开高台时的瞬时速度大小和高台离地面高度分别为(g取10m/s2)( )
 做杂技表演的汽车从高台水平飞出,在空中运动后着地,一架照相机通过多次曝光,拍摄得到汽车在着地前后一段时间内的运动照片,并且汽车刚好到达地面时拍到一次.如图所示,已知汽车长度为3.6m,相邻两次曝光时间间隔相等,由照片(图中实线是用笔画的正方形的格子)可推算出汽车离开高台时的瞬时速度大小和高台离地面高度分别为(g取10m/s2)( )
做杂技表演的汽车从高台水平飞出,在空中运动后着地,一架照相机通过多次曝光,拍摄得到汽车在着地前后一段时间内的运动照片,并且汽车刚好到达地面时拍到一次.如图所示,已知汽车长度为3.6m,相邻两次曝光时间间隔相等,由照片(图中实线是用笔画的正方形的格子)可推算出汽车离开高台时的瞬时速度大小和高台离地面高度分别为(g取10m/s2)( )| A. | 18m/s;11.25 m | B. | 18m/s;7.2m | C. | 12m/s;11.25m | D. | 12m/s;7.2 m |
16.一颗运行中的人造地球卫星,若它到地心的距离为r时,所受万有引力为F,则它到地心的距离为2r时,所受万有引力为( )
| A. | $\frac{1}{4}$F | B. | $\frac{1}{2}$F | C. | 4F | D. | 2F |
 如图所示,不可伸长的轻绳跨过轻质定滑轮,右端系着质量m=2kg的物体,开始时两侧绳子伸直,而物体静止于地面.现用F=30N竖直向下的恒力将A点向下拉动h=2.25m,此时m的速度是4.74m/s如果此时立即立即撤去F,m落回地面时速度大小是8.22m/s.(不计空气阻力,不计滑轮轴处摩擦)
如图所示,不可伸长的轻绳跨过轻质定滑轮,右端系着质量m=2kg的物体,开始时两侧绳子伸直,而物体静止于地面.现用F=30N竖直向下的恒力将A点向下拉动h=2.25m,此时m的速度是4.74m/s如果此时立即立即撤去F,m落回地面时速度大小是8.22m/s.(不计空气阻力,不计滑轮轴处摩擦) 如图所示,一条长L=5m的小木船,其质量M=100kg,静止在湖边附近的水面上,船身垂直于湖岸,船面可看作水平面,并且比湖岸高出h=0.8m在船尾处站着一个质量m=50kg的人.某时刻该人以相对于岸2m/s2的加速度向船头加速跑去,当它跑到船头时相对于岸的速度为v′,并以这个速度沿水平方向离开船跳向岸边,该人恰好落到湖岸上.已知船在水中运动时受到水的恒定阻力,f=50N,重力加速度g=10m/s2,求:
如图所示,一条长L=5m的小木船,其质量M=100kg,静止在湖边附近的水面上,船身垂直于湖岸,船面可看作水平面,并且比湖岸高出h=0.8m在船尾处站着一个质量m=50kg的人.某时刻该人以相对于岸2m/s2的加速度向船头加速跑去,当它跑到船头时相对于岸的速度为v′,并以这个速度沿水平方向离开船跳向岸边,该人恰好落到湖岸上.已知船在水中运动时受到水的恒定阻力,f=50N,重力加速度g=10m/s2,求: 如图所示,水平面上OA部分粗糙,其他部分光滑.轻弹簧一端固定,另一端与质量为M的小滑块连接,开始时滑块静止在O点,弹簧处于原长.一质量为m的子弹以大小为v0的速度水平向右射入滑块,并留在滑块中,子弹打击滑块的时间极短,可忽略不计.之后,滑块向右运动并通过A点,返回后恰好停在出发点O处.求:
如图所示,水平面上OA部分粗糙,其他部分光滑.轻弹簧一端固定,另一端与质量为M的小滑块连接,开始时滑块静止在O点,弹簧处于原长.一质量为m的子弹以大小为v0的速度水平向右射入滑块,并留在滑块中,子弹打击滑块的时间极短,可忽略不计.之后,滑块向右运动并通过A点,返回后恰好停在出发点O处.求: 如图所示,水平传送带长L=16m,始终以4m/s的速度运动,现将一个小物体从传送带的左端由静止释放,已知物体与传送带间的动摩擦因数为0.2,g取10m/s2,求物体从左端运动到右端所需的时间.
如图所示,水平传送带长L=16m,始终以4m/s的速度运动,现将一个小物体从传送带的左端由静止释放,已知物体与传送带间的动摩擦因数为0.2,g取10m/s2,求物体从左端运动到右端所需的时间.