题目内容
15.在太阳系中有一颗行星的半径为R,若在该星球表面以初速度v0竖直上抛出一物体,该物体上升的最大高度为H.已知该物体所受的其他力与行星对它的万有引力相比较可忽略不计.则根据这些条件,不可以求出的物理量是( )| A. | 该行星的密度 | B. | 该行星的自转周期 | ||
| C. | 该星球的第一宇宙速度 | D. | 该行星附近运行的卫星的最小周期 |
分析 根据竖直上抛运动,求出星球表面的重力加速度.根据万有引力提供向心力求在该星球表面附近绕该星球做匀速圆周运动卫星的周期和该星球的第一宇宙速度.
解答 解:A、在该星球表面以初速度v0竖直上抛出一物体,则该物体上升的最大高度为H.
由v02=2gH,得 g=$\frac{{{v}_{0}}^{2}}{2H}$,即可求得该行星表面的重力加速度,
根据GM=gR2知,行星的质量M=$\frac{g{R}^{2}}{G}$,则行星的密度$ρ=\frac{M}{V}=\frac{\frac{g{R}^{2}}{G}}{\frac{4π{R}^{3}}{3}}=\frac{3g}{4πGR}$,故A正确.
B、行星的自转周期与行星的本身有关,根据题意无法求出,故B错误.
C、根据$mg=m\frac{{v}^{2}}{R}$,则该星球的第一宇宙速度v=$\sqrt{gR}$,故C正确.
D、行星附近运行的卫星的速度最大,周期最小,则最小周期就是在该星球表面附近绕该星球做匀速圆周运动的周期,所以最小周期是 T=$\frac{2πR}{v}$,v等于第一宇宙速度,故D正确.
本题选不能求出的,故选:B.
点评 解决本题得关键掌握万有引力提供向心力.重力加速度g是联系星球表面的物体运动和天体运动的桥梁.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
6. 如图所示,一根L形的铁杆可绕墙上的水平轴自由转动,另一端在粗糙平板上,向左拉和向右匀速拉动木板所需要的力分别为F1和F2,那么( )
如图所示,一根L形的铁杆可绕墙上的水平轴自由转动,另一端在粗糙平板上,向左拉和向右匀速拉动木板所需要的力分别为F1和F2,那么( )
 如图所示,一根L形的铁杆可绕墙上的水平轴自由转动,另一端在粗糙平板上,向左拉和向右匀速拉动木板所需要的力分别为F1和F2,那么( )
如图所示,一根L形的铁杆可绕墙上的水平轴自由转动,另一端在粗糙平板上,向左拉和向右匀速拉动木板所需要的力分别为F1和F2,那么( )| A. | F1>F2 | B. | F1<F2 | ||
| C. | F1=F2 | D. | 无法确定F1和F2的大小 |
3. 如图所示,A、B、C、D是匀强电场中的一个正方形的四个顶点,已知A、B、C三点电势分别是20V、4V、-4V,则D点电势是( )
如图所示,A、B、C、D是匀强电场中的一个正方形的四个顶点,已知A、B、C三点电势分别是20V、4V、-4V,则D点电势是( )
 如图所示,A、B、C、D是匀强电场中的一个正方形的四个顶点,已知A、B、C三点电势分别是20V、4V、-4V,则D点电势是( )
如图所示,A、B、C、D是匀强电场中的一个正方形的四个顶点,已知A、B、C三点电势分别是20V、4V、-4V,则D点电势是( )| A. | 4V | B. | 8V | C. | 12V | D. | 16V |
10. 如图所示,木板长L=1.6m,质量M=4.0kg,上表面光滑,下表面与地面间的动摩擦因数为μ=0.4.质量m=1.0kg的小滑块(视为质点)放在木板的右端,开始时木板与物块均处于静止状态,现给木板以向右的初速度v0,重力加速度g取10m/s2,则( )
如图所示,木板长L=1.6m,质量M=4.0kg,上表面光滑,下表面与地面间的动摩擦因数为μ=0.4.质量m=1.0kg的小滑块(视为质点)放在木板的右端,开始时木板与物块均处于静止状态,现给木板以向右的初速度v0,重力加速度g取10m/s2,则( )
 如图所示,木板长L=1.6m,质量M=4.0kg,上表面光滑,下表面与地面间的动摩擦因数为μ=0.4.质量m=1.0kg的小滑块(视为质点)放在木板的右端,开始时木板与物块均处于静止状态,现给木板以向右的初速度v0,重力加速度g取10m/s2,则( )
如图所示,木板长L=1.6m,质量M=4.0kg,上表面光滑,下表面与地面间的动摩擦因数为μ=0.4.质量m=1.0kg的小滑块(视为质点)放在木板的右端,开始时木板与物块均处于静止状态,现给木板以向右的初速度v0,重力加速度g取10m/s2,则( )| A. | 小滑块的加速度为零 | B. | 木板的加速度大小为4m/s2 | ||
| C. | 若v0=2m/s,小滑块将从木板上掉下 | D. | 若v0=5m/s,小滑块将从木板上掉下 |
5. 一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示.设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,合外力从开始至t0时刻做的功是W1,从t0至2t0时刻做的功是W2,则( )
一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示.设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,合外力从开始至t0时刻做的功是W1,从t0至2t0时刻做的功是W2,则( )
 一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示.设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,合外力从开始至t0时刻做的功是W1,从t0至2t0时刻做的功是W2,则( )
一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示.设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,合外力从开始至t0时刻做的功是W1,从t0至2t0时刻做的功是W2,则( )| A. | x1=9x2,v2=5v1 | B. | x2=5x1,v2=3v1 | C. | x2=5x1,W2=8W1 | D. | v2=3v1,W2=9W1 |

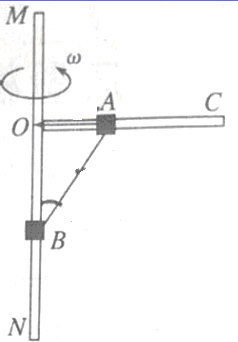 如图所示,光滑圆杆MN段竖直,OC段水平且与MN相接于O点,两杆分别套有质量为m的环A和质量为2m的环B,两环的内径比杆的直径稍大,A、B用长为2L的轻绳连接,A和O点用长为L的轻绳连接,现让装置绕竖直杆MN做匀速圆周运动,当ω=$\sqrt{\frac{2g}{L}}$时,OA段绳刚好要断,AB段绳能承受的拉力足够大,求:
如图所示,光滑圆杆MN段竖直,OC段水平且与MN相接于O点,两杆分别套有质量为m的环A和质量为2m的环B,两环的内径比杆的直径稍大,A、B用长为2L的轻绳连接,A和O点用长为L的轻绳连接,现让装置绕竖直杆MN做匀速圆周运动,当ω=$\sqrt{\frac{2g}{L}}$时,OA段绳刚好要断,AB段绳能承受的拉力足够大,求: 虚线MN为足够大的光滑水平面上的一条界线,界线的右侧是力的作用区.OP为力的作用区内一条直线,OP与界线MN夹角为α.可视为质点的不同小球,沿光滑水平面从界线的O点不断地射入力的作用区内,小球一进入力的作用区就受到水平恒力作用,水平恒力方向平行于MN且由M指向N,恒力大小与小球的重力成正比,比例系数为k N/kg,试求:
虚线MN为足够大的光滑水平面上的一条界线,界线的右侧是力的作用区.OP为力的作用区内一条直线,OP与界线MN夹角为α.可视为质点的不同小球,沿光滑水平面从界线的O点不断地射入力的作用区内,小球一进入力的作用区就受到水平恒力作用,水平恒力方向平行于MN且由M指向N,恒力大小与小球的重力成正比,比例系数为k N/kg,试求: 如图所示,物体质量为2kg,光滑的动滑轮质量不计,今用一竖直向上的恒力向上拉,使物体匀速上升4m距离,则在这一过程中拉力做的功为80J.
如图所示,物体质量为2kg,光滑的动滑轮质量不计,今用一竖直向上的恒力向上拉,使物体匀速上升4m距离,则在这一过程中拉力做的功为80J.