��Ŀ����
19��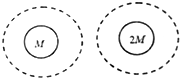 ��ѧ��Ԥ������ϵ���������ǵ��������Ϊ2����-3����֮�䣬����������һ��δ֪���ǣ���뾶�͵���뾶��ͬ��������ȴ�ǵ���������������������ϵ�����a��δ֪�����ϵ�����b�������ľ�����ͬ��������
��ѧ��Ԥ������ϵ���������ǵ��������Ϊ2����-3����֮�䣬����������һ��δ֪���ǣ���뾶�͵���뾶��ͬ��������ȴ�ǵ���������������������ϵ�����a��δ֪�����ϵ�����b�������ľ�����ͬ��������| A�� | ����a������b�����ٶ�֮��Ϊ$\frac{1}{\sqrt{2}}$ | |
| B�� | ����a������b�����ٶ�֮��Ϊ$\frac{1}{\sqrt{8}}$ | |
| C�� | ����a������b������֮��Ϊ$\sqrt{2}$��1 | |
| D�� | ����a������b�����ļ��ٶ�֮��Ϊ1��2 |
���� �������������������������ֱ�������������ٶȵı���ʽ����������ٶ�֮�ȣ��������ڹ�ʽ������֮�ȣ������ļ��ٶȹ�ʽ��������ļ��ٶ�֮�ȣ�
��� �⣺AB���������������������������ã�
������a��G$\frac{M{m}_{a}}{{r}^{2}}$=${m}_{a}\frac{{v}_{a}^{2}}{r}$���� va=$\sqrt{\frac{GM}{r}}$
������b��G$\frac{2M{m}_{b}}{{r}^{2}}$=${m}_{b}\frac{{v}_{b}^{2}}{r}$���� vb=$\sqrt{\frac{2GM}{r}}$���ɵ� va��vb=1��$\sqrt{2}$����A��ȷ��B����
C������a������b������֮��Ϊ Ta��Tb=$\frac{2��r}{{v}_{a}}$��$\frac{2��r}{{v}_{b}}$=$\sqrt{2}$��1����C��ȷ��
D������a������b�����ļ��ٶ�֮��Ϊ aa��ab=$\frac{{v}_{a}^{2}}{r}$��$\frac{{v}_{b}^{2}}{r}$=1��2����D��ȷ��
��ѡ��ACD
���� �������Ĺؼ�Ҫ���������˶���ģ�ͣ�ץס��������������������һ˼·���Ƶ������ٶȡ����ڵȵı���ʽ��

��ϰ��ϵ�д�
 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
�����Ŀ
8���ݱ�����2012��6��28�գ����칬һ�š��롰���۾źš����˷ɴ�������ѽ������߶�Ϊ370km����������Բ������ȴ�ǣ�֡�����ʮ�š����˷ɴ���2012��11��19��6ʱ53�֣��ҹ���̫ԭ���Ƿ������Ľ�������һ�š�c���ǣ�HJ-1C���������ղ��������߶�Ϊ499km��Ԥ��Բ���������˵����ȷ���ǣ�������
| A�� | HJ-1C�ķ����ٶȴ���11.2km/s | |
| B�� | ���칬һ�š��Ķ��ܴ���HJ-1C�Ķ��� | |
| C�� | ���칬һ�š������ڴ���HJ-1C������ | |
| D�� | ���칬һ�š��Ľ��ٶȴ���HJ-1C�Ľ��ٶ� |
7��A��B���ҿ�ͧ�ں�����������Բ���˶�������ͬ��ʱ���ڣ�����ͨ����·��֮����4��3���˶�����ı�ĽǶ�֮��Ϊ3��2�����ǵ����ļ��ٶ�֮��Ϊ��������
| A�� | 2��1 | B�� | 3��2 | C�� | 4��3 | D�� | 8��9 |
11����ͼ��ʾΪijһ��Դ��U-I���ߣ���ͼ��֪��������


| A�� | ��Դ�綯��Ϊ2.0 V | |
| B�� | ��Դ����Ϊ$\frac{1}{3}$�� | |
| C�� | ��Դ��·ʱ����Ϊ6.0A | |
| D�� | ��··�˵�ѹΪ1.0 Vʱ����·�е���Ϊ5.0 A |
8�� ��ͼ��ʾһ����е���IJ�ԴS�������˶��������ͼ�е�Բ��ʾ��е���IJ��棬A��B��C��D���ĸ��۲��ߵ�λ�ã���ͼ���Կ�����������
��ͼ��ʾһ����е���IJ�ԴS�������˶��������ͼ�е�Բ��ʾ��е���IJ��棬A��B��C��D���ĸ��۲��ߵ�λ�ã���ͼ���Կ�����������
 ��ͼ��ʾһ����е���IJ�ԴS�������˶��������ͼ�е�Բ��ʾ��е���IJ��棬A��B��C��D���ĸ��۲��ߵ�λ�ã���ͼ���Կ�����������
��ͼ��ʾһ����е���IJ�ԴS�������˶��������ͼ�е�Բ��ʾ��е���IJ��棬A��B��C��D���ĸ��۲��ߵ�λ�ã���ͼ���Կ�����������| A�� | ��Դ������A�˶� | B�� | ��Դ������C�˶� | ||
| C�� | B��Ĺ۲��߽��յ���Ƶ����� | D�� | D��Ĺ۲��߽��յ���Ƶ����� |
9�� ij����������ˮƽ����������г�˶�����λ��x��ʱ��t�仯�Ĺ�ϵΪx=A sin��t����ͼ����ͼ��ʾ������˵������ȷ���ǣ�������
ij����������ˮƽ����������г�˶�����λ��x��ʱ��t�仯�Ĺ�ϵΪx=A sin��t����ͼ����ͼ��ʾ������˵������ȷ���ǣ�������
 ij����������ˮƽ����������г�˶�����λ��x��ʱ��t�仯�Ĺ�ϵΪx=A sin��t����ͼ����ͼ��ʾ������˵������ȷ���ǣ�������
ij����������ˮƽ����������г�˶�����λ��x��ʱ��t�仯�Ĺ�ϵΪx=A sin��t����ͼ����ͼ��ʾ������˵������ȷ���ǣ�������| A�� | �����ڵ�1sĩ���3sĩ�ij�����ͬ | |
| B�� | ��г�˶��Ľ��ٶȦ�=$\frac{��}{4}$rad/s | |
| C�� | ��3sĩ���ӵ�λ�ƴ�СΪ$\frac{\sqrt{2}}{2}$A | |
| D�� | �ӵ�3sĩ����5sĩ�����ӵ��ٶȷ������仯 |
 ��ͼ��ʾΪһС����ƽ���˶���������Ƭ��һ���֣�ͼ��ÿ����������ı߳���Ϊ4.90cm����ô������Ƭʱ��������Ƶ����10Hz��С��ƽ�ij��ٶ�Ϊ0.98m/s��g=9.8m/s2��
��ͼ��ʾΪһС����ƽ���˶���������Ƭ��һ���֣�ͼ��ÿ����������ı߳���Ϊ4.90cm����ô������Ƭʱ��������Ƶ����10Hz��С��ƽ�ij��ٶ�Ϊ0.98m/s��g=9.8m/s2��