题目内容
4. 如图所示为一小球做平抛运动的闪光照片的一部分,图中每个背景方格的边长均为4.90cm.那么拍摄照片时所用闪光频率是10Hz,小球平抛的初速度为0.98m/s(g=9.8m/s2)
如图所示为一小球做平抛运动的闪光照片的一部分,图中每个背景方格的边长均为4.90cm.那么拍摄照片时所用闪光频率是10Hz,小球平抛的初速度为0.98m/s(g=9.8m/s2)
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据竖直方向上连续相等时间内的位移之差等于恒量求出相等的时间间隔,根据水平位移和时间间隔求出小球平抛运动的初速度.
解答 解:根据△y=2L=gT2得:T=$\sqrt{\frac{2L}{g}}$=$\sqrt{\frac{2×0.049}{9.8}}$s=0.1s,
则闪光频率为:f=$\frac{1}{T}$=10Hz.
小球平抛运动的初速度为:v0=$\frac{2L}{T}$=$\frac{2×0.049}{0.1}$m/s=0.98m/s.
故答案为:10,0.98.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式和推论灵活求解.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
12. 质量为m的小球由轻绳a和b分别系于一轻质木架上的A点和C点.如图所示,当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,绳a在竖直方向,绳b在水平方向,当小球运动到图示位置时,绳b被烧断的同时木架停止转动,则( )
质量为m的小球由轻绳a和b分别系于一轻质木架上的A点和C点.如图所示,当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,绳a在竖直方向,绳b在水平方向,当小球运动到图示位置时,绳b被烧断的同时木架停止转动,则( )
 质量为m的小球由轻绳a和b分别系于一轻质木架上的A点和C点.如图所示,当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,绳a在竖直方向,绳b在水平方向,当小球运动到图示位置时,绳b被烧断的同时木架停止转动,则( )
质量为m的小球由轻绳a和b分别系于一轻质木架上的A点和C点.如图所示,当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,绳a在竖直方向,绳b在水平方向,当小球运动到图示位置时,绳b被烧断的同时木架停止转动,则( )| A. | 绳a对小球拉力不变 | B. | 绳a对小球拉力增大 | ||
| C. | 小球一定前后摆动 | D. | 小球可能在竖直平面内做圆周运动 |
19.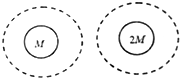 科学家预测银河系中所有行星的数量大概为2万亿-3万亿之间,若宇宙中有一颗未知行星,其半径和地球半径相同,但质量却是地球质量的两倍,如地球上的卫星a和未知行星上的卫星b距离地面的距离相同,则( )
科学家预测银河系中所有行星的数量大概为2万亿-3万亿之间,若宇宙中有一颗未知行星,其半径和地球半径相同,但质量却是地球质量的两倍,如地球上的卫星a和未知行星上的卫星b距离地面的距离相同,则( )
 科学家预测银河系中所有行星的数量大概为2万亿-3万亿之间,若宇宙中有一颗未知行星,其半径和地球半径相同,但质量却是地球质量的两倍,如地球上的卫星a和未知行星上的卫星b距离地面的距离相同,则( )
科学家预测银河系中所有行星的数量大概为2万亿-3万亿之间,若宇宙中有一颗未知行星,其半径和地球半径相同,但质量却是地球质量的两倍,如地球上的卫星a和未知行星上的卫星b距离地面的距离相同,则( )| A. | 卫星a和卫星b的线速度之比为$\frac{1}{\sqrt{2}}$ | |
| B. | 卫星a和卫星b的线速度之比为$\frac{1}{\sqrt{8}}$ | |
| C. | 卫星a和卫星b的周期之比为$\sqrt{2}$:1 | |
| D. | 卫星a和卫星b的向心加速度之比为1:2 |
9.质量为m、速度为v的A球跟质量为3m、静止的B球发生正碰.碰撞可能是弹性的,也可能是非弹性的,则碰撞后B球的速度可能为( )
| A. | 0.6V | B. | 0.4V | C. | 0.3V | D. | 0.2V |
13.一物体自t=0时开始做直线运动,其速度图线如图所示.下列选项正确的是( )


| A. | 在0~6 s内,物体离出发点最远为30 m | |
| B. | 在0~6 s内,物体经过的路程为30 m | |
| C. | 在0~4 s内,物体的平均速率为7.5 m/s | |
| D. | 在5~6 s内,物体所受的合外力做负功 |
14. 如图甲所示,水平放置的平行金属导轨连接一个平行板电容器C和电阻R,导体棒MN放在导轨上且接触良好,整个装置放于垂直导轨平面的磁场中,磁感应强度B的变化情况如图乙所示(图甲中磁感应强度方向为正),MN始终保持静止,则0~t2时间内( )
如图甲所示,水平放置的平行金属导轨连接一个平行板电容器C和电阻R,导体棒MN放在导轨上且接触良好,整个装置放于垂直导轨平面的磁场中,磁感应强度B的变化情况如图乙所示(图甲中磁感应强度方向为正),MN始终保持静止,则0~t2时间内( )
 如图甲所示,水平放置的平行金属导轨连接一个平行板电容器C和电阻R,导体棒MN放在导轨上且接触良好,整个装置放于垂直导轨平面的磁场中,磁感应强度B的变化情况如图乙所示(图甲中磁感应强度方向为正),MN始终保持静止,则0~t2时间内( )
如图甲所示,水平放置的平行金属导轨连接一个平行板电容器C和电阻R,导体棒MN放在导轨上且接触良好,整个装置放于垂直导轨平面的磁场中,磁感应强度B的变化情况如图乙所示(图甲中磁感应强度方向为正),MN始终保持静止,则0~t2时间内( )| A. | 电阻R上电流先减小后增大 | B. | 电容器C的b板始终带负电 | ||
| C. | MN所受摩擦力先变小后变大 | D. | MN所受安培力的方向先向左后向右 |
 如图所示,武直10武装直升机的旋翼桨盘面积(桨叶旋转形成的圆面面积)为S,空气密度为ρ,直升机质量为m,重力加速度为g.求直升机悬停在空中时,直升机发动机的功率.
如图所示,武直10武装直升机的旋翼桨盘面积(桨叶旋转形成的圆面面积)为S,空气密度为ρ,直升机质量为m,重力加速度为g.求直升机悬停在空中时,直升机发动机的功率. “太极球”是近年来在广大市民中较流行的一种健身器材,做该项运动时,健身者半马步站立,手持太极球拍,拍上放一橡胶太极球,健身者舞动球拍时,球却不会掉落地上.现将太极球简化成如图所示的平板和小球,熟练的健身者让质量为m的球在竖直面内始终不脱离板而做匀速圆周运动,且在运动到图中的A、B、C、D位置时球与板之间无相对运动的趋势.A为圆周的最高点,C为最低点,B、D与圆心O等高.不计板的重力,则球在C处所受板的弹力大小与在A处所受板的弹力大小之差是2mg.
“太极球”是近年来在广大市民中较流行的一种健身器材,做该项运动时,健身者半马步站立,手持太极球拍,拍上放一橡胶太极球,健身者舞动球拍时,球却不会掉落地上.现将太极球简化成如图所示的平板和小球,熟练的健身者让质量为m的球在竖直面内始终不脱离板而做匀速圆周运动,且在运动到图中的A、B、C、D位置时球与板之间无相对运动的趋势.A为圆周的最高点,C为最低点,B、D与圆心O等高.不计板的重力,则球在C处所受板的弹力大小与在A处所受板的弹力大小之差是2mg. 如图所示为一种加速度仪的示意图.质量为m的振子两端连有劲度系数均为k的轻弹簧,电源的电动势为E,不计内阻,滑动变阻器的总阻值为R,有效长度为L,系统静止时,滑动触头位于滑动变阻器正中,这时电压表指针恰好在刻度盘正中.
如图所示为一种加速度仪的示意图.质量为m的振子两端连有劲度系数均为k的轻弹簧,电源的电动势为E,不计内阻,滑动变阻器的总阻值为R,有效长度为L,系统静止时,滑动触头位于滑动变阻器正中,这时电压表指针恰好在刻度盘正中.