题目内容
7．A、B两艘快艇在湖面上做匀速圆周运动，在相同的时间内，它们通过的路程之比是4：3，运动方向改变的角度之比为3：2，它们的向心加速度之比为（ ）| A． | 2：1 | B． | 3：2 | C． | 4：3 | D． | 8：9 |
分析 根据相同时间内转过的角度之比得出线速度、角速度大小之比，通过a=vω得出向心加速度之比．
解答 解：因为相同时间内它们通过的路程之比是4：3，则线速度之比为4：3；
运动方向改变的角度之比为3：2，则角速度之比为3：2，
根据a=vω得，向心加速度之比为：$\frac{{a}_{A}}{{a}_{B}}=\frac{{v}_{A}{ω}_{A}}{{v}_{B}{ω}_{B}}=\frac{4}{3}×\frac{3}{2}=\frac{2}{1}$．选项A正确，BCD错误
故选：A
点评 解决本题的关键掌握线速度与角速度的定义式，以及知道向心加速度与线速度、角速度的关系．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
16．小船在静水中速度为4m/s，要横渡宽为30m，水流速度为3m/s的河流，下述说法中正确的是（ ）
| A． | 此船不可能渡过此河 | B． | 此船可以垂直河岸到达正对岸 | ||
| C． | 此船的实际速度一定为5m/s | D． | 此船过河的最短时间为7.5 s |
“太极球”是近年来在广大市民中较流行的一种健身器材，做该项运动时，健身者半马步站立，手持太极球拍，拍上放一橡胶太极球，健身者舞动球拍时，球却不会掉落地上．现将太极球简化成如图所示的平板和小球，熟练的健身者让质量为m的球在竖直面内始终不脱离板而做匀速圆周运动，且在运动到图中的A、B、C、D位置时球与板之间无相对运动的趋势．A为圆周的最高点，C为最低点，B、D与圆心O等高．不计板的重力，则球在C处所受板的弹力大小与在A处所受板的弹力大小之差是2mg．
2．
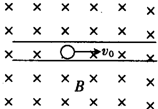在一绝缘、粗糙且足够长得水平管道中有一带电荷量为q、质量为m的带电球体，管道半径略大于球体半径，整个管道处于磁感应强度为B的水平匀强磁场中，磁感应强度方向与管道垂直．现给带电球体一个水平速度v0，则在整个运动过程中，带电球体克服摩擦力所做的功可能为（ ）
在一绝缘、粗糙且足够长得水平管道中有一带电荷量为q、质量为m的带电球体，管道半径略大于球体半径，整个管道处于磁感应强度为B的水平匀强磁场中，磁感应强度方向与管道垂直．现给带电球体一个水平速度v0，则在整个运动过程中，带电球体克服摩擦力所做的功可能为（ ）| A． | 0 | B． | $\frac{1}{2}$mv02 | C． | $\frac{1}{2}$m[v02-（$\frac{mg}{qB}$）2] | D． | $\frac{1}{2}$m[v02+（$\frac{mg}{qB}$）2] |
12．
质量为m的小球由轻绳a和b分别系于一轻质木架上的A点和C点．如图所示，当轻杆绕轴BC以角速度ω匀速转动时，小球在水平面内做匀速圆周运动，绳a在竖直方向，绳b在水平方向，当小球运动到图示位置时，绳b被烧断的同时木架停止转动，则（ ）
质量为m的小球由轻绳a和b分别系于一轻质木架上的A点和C点．如图所示，当轻杆绕轴BC以角速度ω匀速转动时，小球在水平面内做匀速圆周运动，绳a在竖直方向，绳b在水平方向，当小球运动到图示位置时，绳b被烧断的同时木架停止转动，则（ ）| A． | 绳a对小球拉力不变 | B． | 绳a对小球拉力增大 | ||
| C． | 小球一定前后摆动 | D． | 小球可能在竖直平面内做圆周运动 |
19．
科学家预测银河系中所有行星的数量大概为2万亿-3万亿之间，若宇宙中有一颗未知行星，其半径和地球半径相同，但质量却是地球质量的两倍，如地球上的卫星a和未知行星上的卫星b距离地面的距离相同，则（ ）
科学家预测银河系中所有行星的数量大概为2万亿-3万亿之间，若宇宙中有一颗未知行星，其半径和地球半径相同，但质量却是地球质量的两倍，如地球上的卫星a和未知行星上的卫星b距离地面的距离相同，则（ ）| A． | 卫星a和卫星b的线速度之比为$\frac{1}{\sqrt{2}}$ | |
| B． | 卫星a和卫星b的线速度之比为$\frac{1}{\sqrt{8}}$ | |
| C． | 卫星a和卫星b的周期之比为$\sqrt{2}$：1 | |
| D． | 卫星a和卫星b的向心加速度之比为1：2 |
如图所示为一种加速度仪的示意图．质量为m的振子两端连有劲度系数均为k的轻弹簧，电源的电动势为E，不计内阻，滑动变阻器的总阻值为R，有效长度为L，系统静止时，滑动触头位于滑动变阻器正中，这时电压表指针恰好在刻度盘正中．
密闭在钢瓶中的理想气体，温度升高时压强增大．从分子动理论的角度分析，这是由于分子热运动的平均动能增大了．该气体在温度T1、T2时的分子速率分布图象如下图所示，则T1小于（选填“大于”或“小于”）T2．