题目内容
8. 如图所示,质量为m1和m2的木块A、B静置于光滑水平轨道上,A、B之间有一轻弹簧,弹簧与木块A相固连,与木块B不固连.将弹簧压紧并用细线相连,细线突然断开,当B脱离弹簧时,A获得的动量大小为P,B向右运动一段时间后,与竖直固定的挡板碰撞后并反向向左追上A压缩弹簧.已知木块B与挡板碰撞没有能量损失.
如图所示,质量为m1和m2的木块A、B静置于光滑水平轨道上,A、B之间有一轻弹簧,弹簧与木块A相固连,与木块B不固连.将弹簧压紧并用细线相连,细线突然断开,当B脱离弹簧时,A获得的动量大小为P,B向右运动一段时间后,与竖直固定的挡板碰撞后并反向向左追上A压缩弹簧.已知木块B与挡板碰撞没有能量损失.①A和B的质量m1和m2的大小关系应满足什么条件;
②求B追上A并压缩弹簧的过程中弹簧的最大弹性势能.
分析 ①根据B追上A的条件,应用动量守恒定律分析答题;
②应用动量守恒定律与能量守恒定律求出最大弹性势能.
解答 解:①A与B弹开后,A、B的速度大小分别是v1和v2,由动量守恒定律得:
m1v1=m2v2
B追上A须v2>v1,故m1>m2.
②B从光滑曲面滑下后的速度大小仍为v2,当A、B速度相等时弹簧具有最大弹性势能
A与B弹开时有:m1v1=m2v2=P
B追上A时由动量恒定律有:2P=(m1+m2)v
由能量守恒得:$\frac{1}{2}{m}_{1}{{v}_{1}}^{2}+\frac{1}{2}{m}_{2}{{v}_{2}}^{2}-\frac{1}{2}({m}_{1}+{m}_{2}){v}^{2}$=Ep,
解得:${E}_{p}=\frac{({m}_{1}-{m}_{2})^{2}{P}^{2}}{2{m}_{1}{m}_{2}({m}_{1}+{m}_{2})}$.
答:①A和B的质量m1和m2的大小关系应满足m1>m2;
②B追上A并压缩弹簧的过程中弹簧的最大弹性势能为$\frac{({m}_{1}-{m}_{2})^{2}{P}^{2}}{2{m}_{1}{m}_{2}({m}_{1}+{m}_{2})}$.
点评 本题考查了动量守恒定律的应用,分析清楚物体运动过程,应用动量守恒定律与能量守恒定律即可正确解题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
15. 用均匀导线做成的正方形线圈边长为L,正方形的一半放在垂直于纸面向里的匀强磁场中,如图所示,当磁场以$\frac{△B}{△t}$的变化率减弱时,则( )
用均匀导线做成的正方形线圈边长为L,正方形的一半放在垂直于纸面向里的匀强磁场中,如图所示,当磁场以$\frac{△B}{△t}$的变化率减弱时,则( )
 用均匀导线做成的正方形线圈边长为L,正方形的一半放在垂直于纸面向里的匀强磁场中,如图所示,当磁场以$\frac{△B}{△t}$的变化率减弱时,则( )
用均匀导线做成的正方形线圈边长为L,正方形的一半放在垂直于纸面向里的匀强磁场中,如图所示,当磁场以$\frac{△B}{△t}$的变化率减弱时,则( )| A. | 线圈中产生的电动势E=$\frac{△B}{△t}$•$\frac{{L}^{2}}{2}$ | |
| B. | 线圈中a、b两点间的电势差为$\frac{△B}{△t}$$\frac{{L}^{2}}{2}$ | |
| C. | 线圈中a点电势低于b点电势 | |
| D. | 线圈中感应电流方向为acbda |
19.下列说法正确的是( )
| A. | 水波在一个周期内传播的距离是一个波长 | |
| B. | 产生多普勒效应的原因是波源频率发生了变化 | |
| C. | 变化的电场一定产生变化的磁场 | |
| D. | 通过一个狭缝观察日光灯看到的彩色条纹属于光的衍射现象 | |
| E. | 双缝干涉实验中只增大双缝间的距离,干涉条纹间的距离减小 |
3.关于热力学定律和分子动理论,下列说法正确的是( )
| A. | 一定质量的气体吸收热量,其内能可能不变 | |
| B. | 液体温度越高,悬浮颗粒越小,布朗运动越剧烈 | |
| C. | 不可能使热量由低温物体传递到高温物体 | |
| D. | 若两分子间距离增大,分子势能一定增大 | |
| E. | 若两分子间距离减小,分子间引力和斥力都增大 |
13.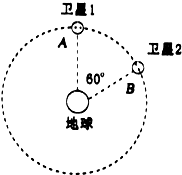 北京时间2015年3月30日2l时52分,我国新一代北斗导航卫星发射升空,卫星顺利进入预定轨道.“北斗”系统中两颗工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置(如图所示).若卫星均沿顺时针运行,地球表面处的重力加速度为g,地球半径为R.不计卫星间的相互作用力.则以下判断中正确的是( )
北京时间2015年3月30日2l时52分,我国新一代北斗导航卫星发射升空,卫星顺利进入预定轨道.“北斗”系统中两颗工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置(如图所示).若卫星均沿顺时针运行,地球表面处的重力加速度为g,地球半径为R.不计卫星间的相互作用力.则以下判断中正确的是( )
 北京时间2015年3月30日2l时52分,我国新一代北斗导航卫星发射升空,卫星顺利进入预定轨道.“北斗”系统中两颗工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置(如图所示).若卫星均沿顺时针运行,地球表面处的重力加速度为g,地球半径为R.不计卫星间的相互作用力.则以下判断中正确的是( )
北京时间2015年3月30日2l时52分,我国新一代北斗导航卫星发射升空,卫星顺利进入预定轨道.“北斗”系统中两颗工作卫星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置(如图所示).若卫星均沿顺时针运行,地球表面处的重力加速度为g,地球半径为R.不计卫星间的相互作用力.则以下判断中正确的是( )| A. | 这两颗卫星的加速度大小相等,均为$\frac{Rg}{r}$ | |
| B. | 这两颗卫星的线速度大小相等,均为$\sqrt{gr}$ | |
| C. | 卫星1向后喷气就一定能追上卫星2 | |
| D. | 卫星1由位置A运动到位置B所需的时间为$\frac{πr}{3Rg}$$\sqrt{gr}$ |
20. 某横波在介质中沿x轴正方向传播t=0时刻,P点开始向y轴正方向运动,经t=0.2s.P点第一次到达正方向最大位移处,某时刻形成的波形如图所示,下列说法正确的是( )
某横波在介质中沿x轴正方向传播t=0时刻,P点开始向y轴正方向运动,经t=0.2s.P点第一次到达正方向最大位移处,某时刻形成的波形如图所示,下列说法正确的是( )
 某横波在介质中沿x轴正方向传播t=0时刻,P点开始向y轴正方向运动,经t=0.2s.P点第一次到达正方向最大位移处,某时刻形成的波形如图所示,下列说法正确的是( )
某横波在介质中沿x轴正方向传播t=0时刻,P点开始向y轴正方向运动,经t=0.2s.P点第一次到达正方向最大位移处,某时刻形成的波形如图所示,下列说法正确的是( )| A. | 该横波的波速为5m/s | |
| B. | 质点Q与质点N都运动起来后,它们的运动方向总相反 | |
| C. | 在0.2s的时间内质点M通过的路程为lm | |
| D. | 从图示时刻再过2.6s,质点M处于平衡位置,且正沿y轴负方向运动 |
17. 如图所示,足够长金属导轨竖直放置,金属棒ab、cd均通过棒两端的环套在金属导轨上并与导轨保持良好的接触?虚线上方有垂直纸面向里的匀强磁场,虚线下方有竖直向下的匀强磁场.ab、cd棒与导轨间动摩擦因数均为μ,两棒总电阻为R,导轨电阻不计.开始两棒均静止在图示位置,当cd棒无初速释放,同时对ab棒施加竖直向上的拉力F,沿导轨向上做匀加速运动.则( )
如图所示,足够长金属导轨竖直放置,金属棒ab、cd均通过棒两端的环套在金属导轨上并与导轨保持良好的接触?虚线上方有垂直纸面向里的匀强磁场,虚线下方有竖直向下的匀强磁场.ab、cd棒与导轨间动摩擦因数均为μ,两棒总电阻为R,导轨电阻不计.开始两棒均静止在图示位置,当cd棒无初速释放,同时对ab棒施加竖直向上的拉力F,沿导轨向上做匀加速运动.则( )
 如图所示,足够长金属导轨竖直放置,金属棒ab、cd均通过棒两端的环套在金属导轨上并与导轨保持良好的接触?虚线上方有垂直纸面向里的匀强磁场,虚线下方有竖直向下的匀强磁场.ab、cd棒与导轨间动摩擦因数均为μ,两棒总电阻为R,导轨电阻不计.开始两棒均静止在图示位置,当cd棒无初速释放,同时对ab棒施加竖直向上的拉力F,沿导轨向上做匀加速运动.则( )
如图所示,足够长金属导轨竖直放置,金属棒ab、cd均通过棒两端的环套在金属导轨上并与导轨保持良好的接触?虚线上方有垂直纸面向里的匀强磁场,虚线下方有竖直向下的匀强磁场.ab、cd棒与导轨间动摩擦因数均为μ,两棒总电阻为R,导轨电阻不计.开始两棒均静止在图示位置,当cd棒无初速释放,同时对ab棒施加竖直向上的拉力F,沿导轨向上做匀加速运动.则( )| A. | ab棒中的电流方向由b到a | |
| B. | 拉力F的功率不断增大 | |
| C. | cd棒先加速运动后匀速运动 | |
| D. | 力F做的功等于两金属棒产生的电热与增加的机械能之和 |
 如图所示,长为0.5m的细绳一端与一质量为1kg的小球(可看成质点)相连,可绕过O点的水平转轴在竖直面内无摩擦地转动.在最低点给一个5m/s的初速度,使小球恰好能通过最高点完成完整的圆周运动,g取10m/s2求:
如图所示,长为0.5m的细绳一端与一质量为1kg的小球(可看成质点)相连,可绕过O点的水平转轴在竖直面内无摩擦地转动.在最低点给一个5m/s的初速度,使小球恰好能通过最高点完成完整的圆周运动,g取10m/s2求: