��Ŀ����
13��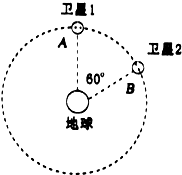 ����ʱ��2015��3��30��2lʱ52�֣��ҹ���һ�������������Ƿ������գ�����˳������Ԥ���������������ϵͳ�����Ź������Ǿ��Ƶ���O������Բ���˶�������뾶Ϊr��ijʱ�����Ź������Ƿֱ�λ�ڹ���ϵ�A��B��λ�ã���ͼ��ʾ���������Ǿ���˳ʱ�����У�������洦���������ٶ�Ϊg������뾶ΪR���������Ǽ������������������ж�����ȷ���ǣ�������
����ʱ��2015��3��30��2lʱ52�֣��ҹ���һ�������������Ƿ������գ�����˳������Ԥ���������������ϵͳ�����Ź������Ǿ��Ƶ���O������Բ���˶�������뾶Ϊr��ijʱ�����Ź������Ƿֱ�λ�ڹ���ϵ�A��B��λ�ã���ͼ��ʾ���������Ǿ���˳ʱ�����У�������洦���������ٶ�Ϊg������뾶ΪR���������Ǽ������������������ж�����ȷ���ǣ�������| A�� | ���������ǵļ��ٶȴ�С��ȣ���Ϊ$\frac{Rg}{r}$ | |
| B�� | ���������ǵ����ٶȴ�С��ȣ���Ϊ$\sqrt{gr}$ | |
| C�� | ����1���������һ����������2 | |
| D�� | ����1��λ��A�˶���λ��B�����ʱ��Ϊ$\frac{��r}{3Rg}$$\sqrt{gr}$ |
���� �������������ṩ������������������������������ǵļ��ٶȺ����ڣ��Ӷ������жϣ����˶��Ĺ����У������������ٶȷ���ֱ������������������
��� �⣺A���������������ṩ�������ã�$\frac{GmM}{{r}^{2}}$=ma��
���a=$\frac{GM}{{r}^{2}}$�����������������������ã�GM=gR2��
�����ǵļ��ٶ�a=$\frac{{gR}^{2}}{{r}^{2}}$��֪���ǵļ��ٶȴ�С��ȣ���A����
B�����������ǵ����ٶȴ�С��ȣ���Ϊv=$\sqrt{\frac{GM}{r}}$=$\sqrt{\frac{{gR}^{2}}{r}}$����B����
C��������1��������������ٶȻ���������1���������˶�����������1������������2����C����
D����$\frac{GmM}{{r}^{2}}$=m$\frac{{4��}^{2}}{{T}^{2}}$r��$\frac{G{Mm}_{0}}{{R}^{2}}$=m0g��
������ã�T=2��$\sqrt{\frac{{r}^{3}}{GM}}$=2��$\sqrt{\frac{{r}^{3}}{{gR}^{2}}}$��
������1��λ��A�˶���λ��B�����ʱ��Ϊ��t=$\frac{T}{6}$=$\frac{��r}{3Rg}$$\sqrt{gr}$����D��ȷ��
��ѡ��D��
���� �������Ĺؼ��������������������������������ṩ���������������ۣ�����������ã�


| A�� | ��A��Ϊ�Ϲ�ĸ���ͼ�� | B�� | ��B��Ϊ�Ϲ�ĸ���ͼ�� | ||
| C�� | ��C��Ϊ���ĸ���ͼ�� | D�� | ��D��Ϊ���ĸ���ͼ�� |
| A�� | ����������ɵ�ϵͳ����������Ӽ�ľ����������С | |
| B�� | Һ��������Ӽ�������Һ���ڲ����Ӽ���룬��Һ������������ | |
| C�� | �Ѻܶ�С�ĵ��������һ�𣬾ͱ���˷Ǿ��� | |
| D�� | �ڶ���������û��Υ�������غ㶨�� |
 ͼ����һ�����ѹ��ԭ������Ȧ����֮��Ϊ10��1����ԭ��Ȧ���˽�����ͼ����ʾ������ʽ�������������Ȧͨ������������ֵR=22���ĸ��ص�����������������ѹ���ͽ���������������������������˵������ȷ���ǣ�������
ͼ����һ�����ѹ��ԭ������Ȧ����֮��Ϊ10��1����ԭ��Ȧ���˽�����ͼ����ʾ������ʽ�������������Ȧͨ������������ֵR=22���ĸ��ص�����������������ѹ���ͽ���������������������������˵������ȷ���ǣ�������| A�� | ��ѹ����ʾ����220V | B�� | ��������ʾ����1.4A | ||
| C�� | ��ѹ��ԭ��Ȧ�����˹�����22W | D�� | ͨ��R�Ľ��������Ƶ����50Hz |
| A�� | mgh | B�� | mgH | C�� | 0 | D�� | $\frac{1}{2}$mv02+mgh |

 ��ͼ��ʾ������Ϊm1��m2��ľ��A��B�����ڹ⻬ˮƽ����ϣ�A��B֮����һ�ᵯ�ɣ�������ľ��A���������ľ��B��������������ѹ������ϸ��������ϸ��ͻȻ�Ͽ�����B���뵯��ʱ��A��õĶ�����СΪP��B�����˶�һ��ʱ�������ֱ�̶��ĵ�����ײ����������Aѹ�����ɣ���֪ľ��B�뵲����ײû��������ʧ��
��ͼ��ʾ������Ϊm1��m2��ľ��A��B�����ڹ⻬ˮƽ����ϣ�A��B֮����һ�ᵯ�ɣ�������ľ��A���������ľ��B��������������ѹ������ϸ��������ϸ��ͻȻ�Ͽ�����B���뵯��ʱ��A��õĶ�����СΪP��B�����˶�һ��ʱ�������ֱ�̶��ĵ�����ײ����������Aѹ�����ɣ���֪ľ��B�뵲����ײû��������ʧ��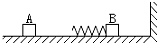 ��ͼ��ʾ���ڹ⻬��ˮƽ���ϣ�����Ϊ2m����A�Գ��ٶ�v0���ҿ�ʼ�˶�������Ϊm������B�����ڹ⻬ˮƽ���ϣ����������һ���ʵ��ɣ�������Aѹ�����ʵ���������A?B�պ���Ծ�ֹʱ������B�����Ҳ���ֱǽ�ϣ�����ǽճ��?��
��ͼ��ʾ���ڹ⻬��ˮƽ���ϣ�����Ϊ2m����A�Գ��ٶ�v0���ҿ�ʼ�˶�������Ϊm������B�����ڹ⻬ˮƽ���ϣ����������һ���ʵ��ɣ�������Aѹ�����ʵ���������A?B�պ���Ծ�ֹʱ������B�����Ҳ���ֱǽ�ϣ�����ǽճ��?��