题目内容
18.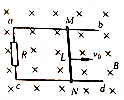 如图所示,两条平行金属导轨ab、cd置于匀强磁场中,磁场方向垂直金属导轨平面,两导轨间的距离L=0.6m,金属杆MN沿两条导轨向右匀速滑动,速度v0=10m/s,产生的感应电动势为3V,已知金属到杆MN的电阻r=1Ω,外接电阻R=8Ω.求:
如图所示,两条平行金属导轨ab、cd置于匀强磁场中,磁场方向垂直金属导轨平面,两导轨间的距离L=0.6m,金属杆MN沿两条导轨向右匀速滑动,速度v0=10m/s,产生的感应电动势为3V,已知金属到杆MN的电阻r=1Ω,外接电阻R=8Ω.求:(1)磁场的磁感应强度大小;
(2)MN两端的电势差,并指出哪点电势高;
(3)金属杆MN受到的安培力的大小和方向.
分析 (1)根据感应电动势公式E=BLv,求磁感应强度大小;
(2)由右手定则判断电势的高低,由欧姆定律求出感应电流,并求解MN两端的电压.
(3)由F=BIL求安培力的大小,由左手定则判断安培力的方向.
解答 解:(1)根据E=BLv0得
B=$\frac{E}{L{v}_{0}}$=$\frac{3}{0.6×10}$=0.5T
(2)电流 I=$\frac{E}{R+r}$=$\frac{3}{8+1}$=0.3A
MN两端的电势差 UMN=IR=2.4V
由右手定则判断得知,M端的电势高.
(3)金属杆MN受到的安培力的大小 F=BIL=0.5×0.3×0.6N=0.09N
方向向左.
答:
(1)磁场的磁感应强度大小是0.5T;
(2)MN两端的电势差为2.4V,M点电势高;
(3)金属杆MN受到的安培力的大小为0.09N,方向向左.
点评 解决本题的关键掌握切割产生感应电动势的大小公式,并能灵活运用.要注意右手定则和左手定则使用条件的不同,不能混淆.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
9.通过归类和比较,有助于理解和掌握新概念、新知识.下列类比不正确的是( )
| A. | 点电荷可以与质点类比,都是理想化模型 | |
| B. | 机械波可以与电磁波类比,两者都可以在真空中传播 | |
| C. | 电场力做功可以与重力做功类比.两种力做功都与路径无关 | |
| D. | 电场线可以与磁感线类比,都是用假想的曲线形象化地描绘“场”的客观存在 |
13.一颗子弹射穿透一块厚度为3.0cm的固定木板后速度减小到原来的$\frac{1}{2}$,假设子弹在穿过木板过程所受的阻力不变,则此后它还能射穿透同样材料木板的厚度最多为( )
| A. | 3.0cm | B. | 1.5cm | C. | 1.0cm | D. | 0.75cm |
3. 有一底面半径为r的筒绕其中心轴线作角速度为ω的匀速圆周运动,如图所示,今用一枪对准筒的轴线射击,当子弹穿过圆筒后发现筒上留下两个弹孔,其两弹孔的连线正好位于筒的一条直径上,则子弹的速度可能值为( )
有一底面半径为r的筒绕其中心轴线作角速度为ω的匀速圆周运动,如图所示,今用一枪对准筒的轴线射击,当子弹穿过圆筒后发现筒上留下两个弹孔,其两弹孔的连线正好位于筒的一条直径上,则子弹的速度可能值为( )
 有一底面半径为r的筒绕其中心轴线作角速度为ω的匀速圆周运动,如图所示,今用一枪对准筒的轴线射击,当子弹穿过圆筒后发现筒上留下两个弹孔,其两弹孔的连线正好位于筒的一条直径上,则子弹的速度可能值为( )
有一底面半径为r的筒绕其中心轴线作角速度为ω的匀速圆周运动,如图所示,今用一枪对准筒的轴线射击,当子弹穿过圆筒后发现筒上留下两个弹孔,其两弹孔的连线正好位于筒的一条直径上,则子弹的速度可能值为( )| A. | $\frac{ωr}{π}$ | B. | $\frac{ωr}{2π}$ | C. | $\frac{2ωr}{π}$ | D. | $\frac{2ωr}{3π}$ |




 如图所示,小球A的质量为m=2kg,固定在L=0.4m的轻细直杆一端,并随杆一起绕杆的另一端O点在竖直在竖直平面内做圆周运动,过最低点时速度为4m/s(不计阻力),求:
如图所示,小球A的质量为m=2kg,固定在L=0.4m的轻细直杆一端,并随杆一起绕杆的另一端O点在竖直在竖直平面内做圆周运动,过最低点时速度为4m/s(不计阻力),求: 如图所示,某同学在跳绳比赛中,1min跳了120次,若每次起跳中有$\frac{4}{5}$时间腾空,该同学体重50kg,则他在跳绳中克服重力做功的平均功率是200W,若他在跳绳的1min内,心脏跳动了60次,每次心跳输送1×10-4m3的血液,其血压(可看做心脏血液压强的平均值)为2×104Pa,则心脏工作的平均功率是2W.
如图所示,某同学在跳绳比赛中,1min跳了120次,若每次起跳中有$\frac{4}{5}$时间腾空,该同学体重50kg,则他在跳绳中克服重力做功的平均功率是200W,若他在跳绳的1min内,心脏跳动了60次,每次心跳输送1×10-4m3的血液,其血压(可看做心脏血液压强的平均值)为2×104Pa,则心脏工作的平均功率是2W. 在光滑绝缘的水平面上,左侧平行极板间有水平方向的匀强电场,右侧圆筒内有竖直方向的匀强磁场,磁感应强度大小为B,俯视图如图所示,圆心为O,半径为R.一质量为m、电荷量为q的带电小球(可视为质点),初始位置在A点,现由静止经电场加速后从C孔沿直径射入磁场区域,小球和圆筒壁的碰撞没有动能和电荷量损失.B、R、m、q均为已知量,圆筒仅有一个出入口C.
在光滑绝缘的水平面上,左侧平行极板间有水平方向的匀强电场,右侧圆筒内有竖直方向的匀强磁场,磁感应强度大小为B,俯视图如图所示,圆心为O,半径为R.一质量为m、电荷量为q的带电小球(可视为质点),初始位置在A点,现由静止经电场加速后从C孔沿直径射入磁场区域,小球和圆筒壁的碰撞没有动能和电荷量损失.B、R、m、q均为已知量,圆筒仅有一个出入口C. 如图所示,光滑水平细杆MN、CD,MN、CD在同一竖直平面内.两杆间距离为h,N、C连线左侧存在有界的电场,电场强度为E.质量为m的带正电的小球P,穿在细杆上,从M端点由静止向N端点运动,在N、C连线中点固定一个带负电的小球,电荷量为Q.在匀强电场中做匀速圆周运动恰好回到C点,且小球P与细杆之间相互绝缘.
如图所示,光滑水平细杆MN、CD,MN、CD在同一竖直平面内.两杆间距离为h,N、C连线左侧存在有界的电场,电场强度为E.质量为m的带正电的小球P,穿在细杆上,从M端点由静止向N端点运动,在N、C连线中点固定一个带负电的小球,电荷量为Q.在匀强电场中做匀速圆周运动恰好回到C点,且小球P与细杆之间相互绝缘.