题目内容
9. 如图所示,两块平行金属板MN、PQ竖直放置,两板间的电势差U=1.6×103V,现将一质量m=3.0×10-2kg、电荷量q=+4.0×10-5C的带电小球从两板左上方的A点以初速度v0=4.0m/s水平抛出,已知A点距两板上端的高度h=0.45m,之后小球恰好从MN板上端内侧M点进入两板间匀强电场,然后沿直线运动到PQ板上的C点,不计空气阻力,取g=10m/s2,求:
如图所示,两块平行金属板MN、PQ竖直放置,两板间的电势差U=1.6×103V,现将一质量m=3.0×10-2kg、电荷量q=+4.0×10-5C的带电小球从两板左上方的A点以初速度v0=4.0m/s水平抛出,已知A点距两板上端的高度h=0.45m,之后小球恰好从MN板上端内侧M点进入两板间匀强电场,然后沿直线运动到PQ板上的C点,不计空气阻力,取g=10m/s2,求:(1)带电小球到达M点时的速度大小;
(2)C点到PQ板上端的距离L;
(3)小球到达C点时的动能Ek.
分析 (1)对A到M过程,运用机械能守恒定律求出带电小球在M点的速度.
(2)抓住小球做直线运动,合力方向与速度方向在同一条直线上,结合平行四边形定则,根据电势差与电场强度的关系求出L的长度.
(3)对M到C的过程运动动能定理,求出小球到达C点时的动能.
解答 解:(1)设小球到达M点时的速度大小为v,从A到M的过程中,由机械能守恒,有:
$\frac{1}{2}m{v}^{2}-\frac{1}{2}m{{v}_{0}}^{2}=mgh$,
得$v=\sqrt{{{v}_{0}}^{2}+2gh}=\sqrt{16+2×10×0.45}$m/s=5m/s.
(2)设小球到达M点时的速度方向与MN板间的夹角为θ,则有:
$sinθ=\frac{{v}_{0}}{v}=0.8$--------①
在两平行板间运动时,小球受水平方向的电场力和竖直向下的重力作用,因为小球在电场内做直线运动,有动力学知识可知,小球受到的电场力方向水平向右,合力方向与速度的方向一致.设极板间的电场强度为E、极板间距离为d,则有
$tanθ=\frac{qE}{mg}$------②
U=Ed------③
L=dcotθ------④
联立①②③④四式,代入数据,可解得C点到PQ板上端的距离为:
L=$\frac{qU}{mgta{n}^{2}θ}$,
代入数据解得:L=0.12m.
(3)从M到C的过程中,由动能定理,有:
${E}_{k}-\frac{1}{2}m{v}^{2}=qU+mgL$,
代入数据,可求得小球到达C点时的动能为:Ek=0.475J.
答:(1)带电小球到达M点时的速度大小为5m/s;
(2)C点到PQ板上端的距离L为0.12m;
(3)小球到达C点时的动能为0.475J.
点评 掌握物体做直线运动的条件和正确的受力分析和做功分析运用动能定理求解是解决本题的关键.

 阅读快车系列答案
阅读快车系列答案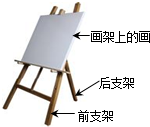 如图所示,水平地面上放着一个画架,它的前支架是固定而后支架可前后移动,画架上静止放着一幅重为G的画.下列说法正确的是( )
如图所示,水平地面上放着一个画架,它的前支架是固定而后支架可前后移动,画架上静止放着一幅重为G的画.下列说法正确的是( )| A. | 画架对画的作用力大于G | |
| B. | 画架对画的作用力大小等于G | |
| C. | 若后支架缓慢向后退则画架对画作用力变大 | |
| D. | 若后支架缓慢向后退则画架对画作用力不变 |
 如图a、b、c为三个完全相同的带正电荷的油滴,在真空中从相同高度由静止下落到同一水平面,a下落中有水平匀强电场,b下落中有水平向里的匀强磁场,三油滴落地时间设为ta、tb、tc,落地时速度分别va、vb、vc,则( )
如图a、b、c为三个完全相同的带正电荷的油滴,在真空中从相同高度由静止下落到同一水平面,a下落中有水平匀强电场,b下落中有水平向里的匀强磁场,三油滴落地时间设为ta、tb、tc,落地时速度分别va、vb、vc,则( )| A. | ta=tb=tc,va=vb=vc | B. | ta=tb=tc,va>vb=vc | ||
| C. | tb>ta=tc,va=vb=vc | D. | tb>ta=tc,va>vc=vb |
 平面MN、PQ、ST为三个相互平行的界面,Ⅰ、Ⅱ、Ⅲ为三种不同的介质,平面ST的上表面涂有反射层(光线不能通过).某种单色光线射向界面MN后,发生了一系列的反射和折射现象,光路如图所示.则( )
平面MN、PQ、ST为三个相互平行的界面,Ⅰ、Ⅱ、Ⅲ为三种不同的介质,平面ST的上表面涂有反射层(光线不能通过).某种单色光线射向界面MN后,发生了一系列的反射和折射现象,光路如图所示.则( )| A. | 当入射角β适当减小时,光线c、d都可能会消失 | |
| B. | 当入射角β适当增大时,光线d可能会消失 | |
| C. | 对于三种介质,光在介质Ⅱ中的传播速度最小 | |
| D. | 出射光线b、c、d不一定平行 |
 如图所示,a、b两物体的质量分别为m1和m2,由轻质弹簧相连.当用恒力F竖直向上拉着a,使a、b-起向上做匀加速直线运动时,弹簧伸长量为为x1,加速度大小为a1;当用大小仍为F的恒力沿水平方向拉着a,使a、b-起沿光滑水平桌面做匀加速直线运动时,弹簧伸长量为x2,加速度大小为a2.则有( )
如图所示,a、b两物体的质量分别为m1和m2,由轻质弹簧相连.当用恒力F竖直向上拉着a,使a、b-起向上做匀加速直线运动时,弹簧伸长量为为x1,加速度大小为a1;当用大小仍为F的恒力沿水平方向拉着a,使a、b-起沿光滑水平桌面做匀加速直线运动时,弹簧伸长量为x2,加速度大小为a2.则有( )| A. | a1=a2,x1=x2 | B. | a1<a2,x1=x2 | C. | a1=a2,x1>x2 | D. | a1<a2,x1>x2 |

| A. | 750Ω | B. | 760Ω | C. | 1000Ω | D. | 1010Ω |
 如图所示,竖直平面内的一半径R=0.50m的光滑圆弧槽BCD,B点与圆心O等高,一水平面与圆弧槽相接于D点.质量m=0.10kg的小球从B点正上方H=1.20m高处的A点自由下落,由B点进入圆弧轨道,从D点飞出后落在水平面上的Q点,DQ间的距离s=3.2m,球从D点飞出后的运动过程中相对水平面上升的最大高度h=0.80m,取g=10m/s2,不计空气阻力,求:
如图所示,竖直平面内的一半径R=0.50m的光滑圆弧槽BCD,B点与圆心O等高,一水平面与圆弧槽相接于D点.质量m=0.10kg的小球从B点正上方H=1.20m高处的A点自由下落,由B点进入圆弧轨道,从D点飞出后落在水平面上的Q点,DQ间的距离s=3.2m,球从D点飞出后的运动过程中相对水平面上升的最大高度h=0.80m,取g=10m/s2,不计空气阻力,求: 如图所示,物体甲重20N,物体乙重100N,乙与水平桌面间的最大静摩擦力是30N,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.(已知sin 37°=0.6,cos 37°=0.8)求:
如图所示,物体甲重20N,物体乙重100N,乙与水平桌面间的最大静摩擦力是30N,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.(已知sin 37°=0.6,cos 37°=0.8)求: