题目内容
19. 如图所示,电流表示数I=0.75A,电压表示数为U=2V,某一电阻烧断后,电流表读数变为I′=0.8A,电压表示数为U′=3.2V,已知R3=4Ω,不计电压表和电流表对电路的影响.问:
如图所示,电流表示数I=0.75A,电压表示数为U=2V,某一电阻烧断后,电流表读数变为I′=0.8A,电压表示数为U′=3.2V,已知R3=4Ω,不计电压表和电流表对电路的影响.问:(1)发生故障的电阻是哪个?写出判断依据,它的阻值为多少?
(2)电源的电动势和内阻分别为多少?
分析 (1)由题意,电路中某一电阻断路后,两电表的读数都变大,不可能是R3和R2断路,否则变化后电压表或电流表无读数,只可能R1断路.
(2)断路时,电压表读数等于电阻R1的电压,由欧姆定律求出R1.根据闭合电路欧姆定律对发生断路前后两种情况列方程,组成方程组,联立求解电动势和内电阻.
解答 解:(1)因某电阻烧断后,电流表、电压表示数均增大,若R1、R3断路,电流表或电压表无读数,可断定发生故障的电阻是R1.
R1烧断后,伏特表的读数为R2两端的电压,则得:
R2=$\frac{U′}{I′}$=$\frac{3.2}{0.8}$Ω=4Ω
R1烧断前,R3两端电压
U3=IR2-U=0.75×4-2=1(V)
通过R3的电流为 I3=$\frac{{U}_{3}^{\;}}{{R}_{3}^{\;}}$=$\frac{1}{4}$=0.25A
电阻R1的阻值为 R1=$\frac{U}{{I}_{3}^{\;}}$=$\frac{2}{0.25}$=8Ω;
(2)R1烧断前,外电阻为 R外=$\frac{({R}_{1}^{\;}+{R}_{3}^{\;}){R}_{2}^{\;}}{{R}_{1}^{\;}+{R}_{2}^{\;}+{R}_{3}^{\;}}$=$\frac{(8+4)×4}{8+4+4}$Ω=3Ω
总电流为 I0=I+$\frac{U}{{R}_{1}^{\;}}$=0.75+$\frac{2}{8}$=1(A)
由闭合电路欧姆定律得:
E=I0(R外+r),
即 E=1×(3+r)
当R1烧断后,E=I′(R2+r)
即 E=0.8×(4+r)
联立解得:r=1Ω,E=4V;
答:(1)发生故障的电阻是R1.它的阻值为8Ω.
(2)电源的电动势为4V,内阻为1Ω.
点评 本题中涉及故障分析,采用排除法逐一分析.对于电源的电动势和内阻,常常根据两种情况列方程组求解.

 天天向上口算本系列答案
天天向上口算本系列答案
| A. | B质点最初4s做加速运动,后4秒做减速运动 | |
| B. | B质点先沿正方向做直线运动,后沿负方向做直线运动 | |
| C. | 质点以20m/s的速度匀速运动 | |
| D. | A、B两质点在4s末相遇 |
| A. | 位移是标量,路程是矢量 | |
| B. | 在直线运动中,位移的大小和路程一定相同 | |
| C. | 在曲线运动中,位移的大小和路程可能相同 | |
| D. | 位移方向总是与质点平均速度方向一致 |
| A. | 汽车的加速度为2.5m/s2 | B. | 汽车的位移为20 m | ||
| C. | 汽车的平均速度为2.5 m/s | D. | 2 s末汽车的速度为5 m/s |
 如图所示,小球以9m/s的速度匀减速冲上一个斜坡,它到达坡顶的速度为1.8m/s,历时2s,则小球在斜坡上运动的加速度大小、方向为( )
如图所示,小球以9m/s的速度匀减速冲上一个斜坡,它到达坡顶的速度为1.8m/s,历时2s,则小球在斜坡上运动的加速度大小、方向为( )| A. | 3.6 m/s2,沿斜面向上 | B. | 3.6 m/s2,沿斜面向下 | ||
| C. | 4.9 m/s2,沿斜面向上 | D. | 4.9 m/s2,沿斜面向下 |
 一质点沿x轴正方向做直线运动,通过坐标原点时开始计时,其$\frac{x}{t}$-t的图象如图所示,则下列说法正确的是( )
一质点沿x轴正方向做直线运动,通过坐标原点时开始计时,其$\frac{x}{t}$-t的图象如图所示,则下列说法正确的是( )| A. | 质点做匀速直线运动,速度为0.5 m/s | |
| B. | 质点做匀加速直线运动,加速度为0.5 m/s2 | |
| C. | 质点在第1 s内的平均速度0.75 m/s | |
| D. | 质点在1 s末速度为1.5 m/s |
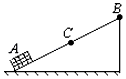 如图所示,物体(可看成质点)以4m/s的初速度自斜面底端A点滑上光滑斜面作匀减速直线运动,途经斜面中点C,到达最高点B.已知在A、C点速度vA:vC=4:3,从C点到B点历时(3-$\sqrt{2}$)s,试求:
如图所示,物体(可看成质点)以4m/s的初速度自斜面底端A点滑上光滑斜面作匀减速直线运动,途经斜面中点C,到达最高点B.已知在A、C点速度vA:vC=4:3,从C点到B点历时(3-$\sqrt{2}$)s,试求:
 在真空中A点有一正电荷Q=2.0×10-4C,把检验电荷q=2.0×10-5C的负电荷置于B点,他们相距离r=2m,如图所示.求:
在真空中A点有一正电荷Q=2.0×10-4C,把检验电荷q=2.0×10-5C的负电荷置于B点,他们相距离r=2m,如图所示.求: