题目内容
3.已知水星和金星两个星球的质量之比和半径之比,可以求出两个星球的( )| A. | 密度之比 | B. | 第一宇宙速度之比 | ||
| C. | 表面重力加速度之比 | D. | 水星和金星绕太阳运动的周期之比 |
分析 根据密度公式$ρ=\frac{M}{V}$,即可判定密度之比;
根据第一宇宙速度表达式v=$\sqrt{\frac{GM}{R}}$,即可求得它们的第一宇宙速度之比;
依据重力等于引力,即可求解表面重力加速度之比;
根据引力提供向心力,结合轨道半径,即可求解周期之比.
解答 解:A、根据密度公式$ρ=\frac{M}{V}$,已知水星和金星两个星球的质量之比和半径之比,因此可求得它们的密度之比.故A正确.
B、根据第一宇宙速度表达式v=$\sqrt{\frac{GM}{R}}$,由于水星和金星的质量和体积之比可知,则可求出水星和金星的第一宇宙速度之比.故B正确.
C、根据g=$\frac{GM}{{R}^{2}}$ 知,知道质量与轨道半径各自之比,可以得出水星和金星的表面加速度之比,故C正确.
D、根据G$\frac{Mm}{{r}^{2}}$=mr$\frac{4{π}^{2}}{{T}^{2}}$ 得,r=$\sqrt{\frac{GM{T}^{2}}{4{π}^{2}}}$,根据水星和金星的轨道半径之比,才可以得出周期之比,由于轨道半径的不知,因此无法确定它们的周期之比,故D错误.
故选:ABC.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,并能灵活运用,本题注意天体的半径与天体的轨道半径不同是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.做简谐运动的振子每次通过同一位置时,相同的物理量是( )
①速度
②加速度
③质量与速度乘积
④动能.
①速度
②加速度
③质量与速度乘积
④动能.
| A. | ①② | B. | ②④ | C. | ②③ | D. | ①④ |
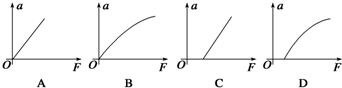
11.物体在水平拉力F作用下,沿x轴方向由坐标原点开始运动,设拉力F随x的变化分别如图甲、乙、丙所示,其中图甲为一半圆图形,对应拉力做功分别为W1、W2、W3,则以下说法正确的是( )
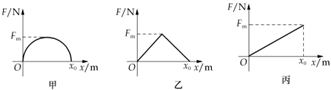

| A. | W1>W2>W3 | B. | W1>W2=W3 | ||
| C. | W1=W2=W3 | D. | 无法比较它们的大小 |
18.在“探究加速度与物体质量、物体受力的关系”活动中:
某同学设计了如图a的实验装置简图,A为小车,B为电火花计时器,C为钩码,D为一端带有定滑轮的长方形木板,实验中认为细绳对小车拉力F等于钩码的总重量,
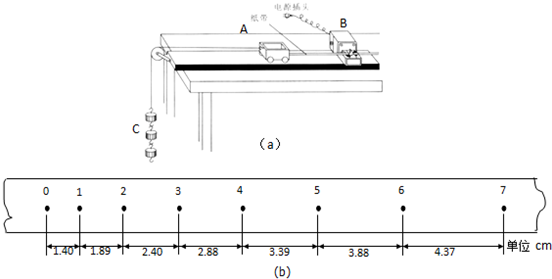
(1)图b是实验中获取的一条纸带的一部分:0、1、2、3、4、5、6、7是计数点,每相邻两计数点间还有4个打点(图中未标出),计数点间的距离如图所示.根据图中数据完成表格中空白处
(2)由(1)中的数据在图c中作出速度-时间图象并由图象求出小车的加速度a=0.496 m/s2 (保留3位有效数字)
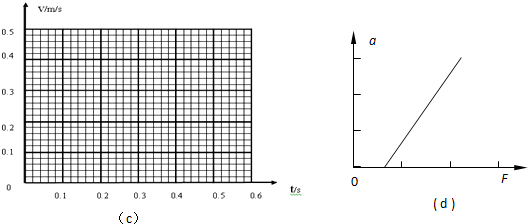
(3)在“探究加速度与力的关系”时,保持小车的质量不变,改变钩码的个数,该同学根据实验数据作出了加速度a与合力F的图线如图d,该图线不通过坐标原点,则开始实验前他应采取的做法是C
A.将木板上不带滑轮的一端适当垫高,使小车在钩码拉动下恰好做匀速运动
B.将木板上不带滑轮的一端适当垫高,使小车在钩码拉动下恰好做匀加速运动
C.将木板上不带滑轮的一端适当垫高,在不挂钩码的情况下使小车恰好做匀速运动
D.将木板上不带滑轮的一端适当垫高,在不挂钩码的情况下使小车恰好做匀加速运动.
某同学设计了如图a的实验装置简图,A为小车,B为电火花计时器,C为钩码,D为一端带有定滑轮的长方形木板,实验中认为细绳对小车拉力F等于钩码的总重量,

(1)图b是实验中获取的一条纸带的一部分:0、1、2、3、4、5、6、7是计数点,每相邻两计数点间还有4个打点(图中未标出),计数点间的距离如图所示.根据图中数据完成表格中空白处
| 计数点 | 1 | 2 | 3 | 4 | 5 | 6 |
| 瞬时速度/(m/s) | 0.165 | 0.215 | 0.314 | 0.364 | 0.413 |

(3)在“探究加速度与力的关系”时,保持小车的质量不变,改变钩码的个数,该同学根据实验数据作出了加速度a与合力F的图线如图d,该图线不通过坐标原点,则开始实验前他应采取的做法是C
A.将木板上不带滑轮的一端适当垫高,使小车在钩码拉动下恰好做匀速运动
B.将木板上不带滑轮的一端适当垫高,使小车在钩码拉动下恰好做匀加速运动
C.将木板上不带滑轮的一端适当垫高,在不挂钩码的情况下使小车恰好做匀速运动
D.将木板上不带滑轮的一端适当垫高,在不挂钩码的情况下使小车恰好做匀加速运动.
15.若宇航员在月球表面附近自高h处以初速度v0水平抛出一个小球,测出小球的水平射程为L.已知月球半径为R,万有引力常量为G.则下列说法正确的是( )
| A. | 月球表面的重力加速度g月=$\frac{h{v}_{0}^{2}}{{L}^{2}}$ | |
| B. | 月球的平均密度ρ=$\frac{3h{v}_{0}^{2}}{2πG{L}^{2}R}$ | |
| C. | 月球的第一宇宙速度v=$\frac{{v}_{0}}{L}$$\sqrt{2h}$ | |
| D. | 月球的质量m月=$\frac{h{R}^{2}{v}_{0}^{2}}{G{L}^{2}}$ |

 黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其它天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.
黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其它天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.