题目内容
13. 某同学通过实验探究动能定理,装置如图所示.
某同学通过实验探究动能定理,装置如图所示.在一倾斜的气势导轨固定在水平面上,已测得导轨总长为L,斜面高h,气势导轨A、B两点各有一个光电门,一带条形遮光片的滑块,已知其质量为M,用一根细绳跨过光滑定滑轮,将滑块与质量为m的钩码相连;现测得遮光条的宽度为d,A点到B点的距离为s,可以认为遮光片通过光电门的平均速度看作通过该位置的瞬时速度,待钩码静止时,将滑块由静止从斜面顶端释放,滑块通过光电门A的时间为t1,通过光电门B的时间为t2.用g表示重力加速度.
(1)则在滑块下滑过程中,滑块在A点的动能为EK1=$\frac{1}{2}M(\frac{d}{{t}_{1}^{\;}})_{\;}^{2}$,在B点的动能为EK2=$\frac{1}{2}M(\frac{d}{{t}_{2}^{\;}})_{\;}^{2}$.(用题中字母表示)
(2)当实验中满足条件M>>m时,可以认为滑块受的合理为$mg+Mg\frac{h}{L}$,则滑块从A运动到B的过程中,合力对滑块做的功为W=$(m+M\frac{h}{L})gs$.(用题中字母表示)
(3)如果试验中$(m+M\frac{h}{L})gs$=$\frac{1}{2}M(\frac{d}{{t}_{2}^{\;}})_{\;}^{2}-\frac{1}{2}M(\frac{d}{{t}_{1}^{\;}})_{\;}^{2}$,则验证了动能定理.(用题中字母表示)
分析 (1)由于光电门的宽度d很小,所以我们用短时间内的平均速度代替瞬时速度,再根据动能表达式求出A、B点的动能;
(2)当M>>m时,绳子中的拉力近似等于钩码的重力,再对滑块运用牛顿第二定律求出合力,再求出合力做功;
(3)要验证动能定理,只需合力做功和动能的变化量相等即可;
解答 解:(1)滑块通过A点的速度为:${v}_{A}^{\;}=\frac{d}{{t}_{1}^{\;}}$
滑块在A点的动能为:${E}_{k1}^{\;}=\frac{1}{2}M{v}_{A}^{2}=\frac{1}{2}M(\frac{d}{{t}_{1}^{\;}})_{\;}^{2}$
滑块通过B点的速度为:${v}_{B}^{\;}=\frac{d}{{t}_{2}^{\;}}$
滑块在B点的动能为:${E}_{k2}^{\;}=\frac{1}{2}M{v}_{B}^{2}=\frac{1}{2}M(\frac{d}{{t}_{2}^{\;}})_{\;}^{2}$
(2)当M>>m时,可以认为绳子的拉力近似等于钩码的重力mg,滑块受到的合力为:${F}_{合}^{\;}=Mgsinθ+T=Mg\frac{h}{L}+mg$
从A到B的过程中,合力对滑块做的功为:${W}_{合}^{\;}={F}_{合}^{\;}s=(mg+Mg\frac{h}{L})s$
(3)从A到B过程中,滑块的合力做功等于动能的变化量,则验证了动能定理
动能变化量为:$△{E}_{k}^{\;}=\frac{1}{2}M{v}_{B}^{2}-\frac{1}{2}M{v}_{A}^{2}=\frac{1}{2}M(\frac{d}{{t}_{2}^{\;}})_{\;}^{2}$$-\frac{1}{2}M(\frac{d}{{t}_{1}^{\;}})_{\;}^{2}$
要验证的表达式为:$(mg+Mg\frac{h}{L})s$═$\frac{1}{2}M(\frac{d}{{t}_{2}^{\;}})_{\;}^{2}-\frac{1}{2}M(\frac{d}{{t}_{1}^{\;}})_{\;}^{2}$
故答案为:(1)$\frac{1}{2}M(\frac{d}{{t}_{1}^{\;}})_{\;}^{2}$,$\frac{1}{2}M(\frac{d}{{t}_{2}^{\;}})_{\;}^{2}$;(2)$mg+Mg\frac{h}{L}$;($mg+Mg\frac{h}{L}$)s;(3)$(mg+Mg\frac{h}{L})s$,$\frac{1}{2}M(\frac{d}{{t}_{2}^{\;}})_{\;}^{2}-\frac{1}{2}M(\frac{d}{{t}_{1}^{\;}})_{\;}^{2}$
点评 明确实验原理是解决实验问题的关键,本实验的关键是两个问题,一个是注意气垫导轨可以忽略摩擦力,再一个是绳子拉力近似等于钩码的重力.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案 如图所示,竖直向上的匀强电场中,绝缘轻质弹簧竖直立于水平地面上,上面放一质量为m的带正电小球,小球与弹簧不连接,施加外力F将小球向下压至某位置静止.现撤去F,小球从静止开始运动到离开弹簧的过程中,( )
如图所示,竖直向上的匀强电场中,绝缘轻质弹簧竖直立于水平地面上,上面放一质量为m的带正电小球,小球与弹簧不连接,施加外力F将小球向下压至某位置静止.现撤去F,小球从静止开始运动到离开弹簧的过程中,( )| A. | 小球与弹簧组成的系统机械能守恒 | B. | 小球的机械能守恒 | ||
| C. | 小球与弹簧组成的系统机械能增加 | D. | 小球的机械能增加 |
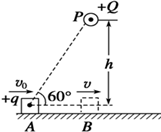 如图所示,在足够长的光滑绝缘水平直线轨道上方的P点,固定一电荷量为+Q的点电荷.一质量为m、带电荷量为+q的物块(可视为质点的检验电荷),从轨道上的A点以初速度v0沿轨道向右运动,当运动到P点正下方B点时速度为v.已知点电荷产生的电场在A点的电势为φ(取无穷远处电势为零),P到物块的重心竖直距离为h,P、A连线与水平轨道的夹角为60°,k为静电常数,下列说法正确的是( )
如图所示,在足够长的光滑绝缘水平直线轨道上方的P点,固定一电荷量为+Q的点电荷.一质量为m、带电荷量为+q的物块(可视为质点的检验电荷),从轨道上的A点以初速度v0沿轨道向右运动,当运动到P点正下方B点时速度为v.已知点电荷产生的电场在A点的电势为φ(取无穷远处电势为零),P到物块的重心竖直距离为h,P、A连线与水平轨道的夹角为60°,k为静电常数,下列说法正确的是( )| A. | 物块在A点的电势能EPA=Qφ | |
| B. | 物块在A点时受到轨道的支持力大小为mg+$\frac{3\sqrt{3}kqQ}{8{h}^{2}}$ | |
| C. | 点电荷+Q产生的电场在B点的电场强度大小EB=K$\frac{q}{{h}^{2}}$ | |
| D. | 点电荷+Q产生的电场在B点的电势φB=$\frac{m}{2q}$(v02-v2)+φ |

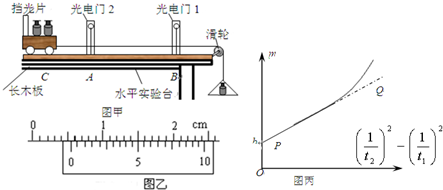
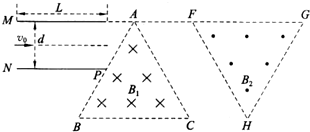
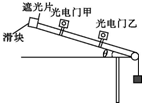 现要用如图所示的实验装置探究“动能定理”:一倾角θ可调的斜面上安装有两个光电门,其中光电门乙固定在斜面上,光电门甲的位置可移动.不可伸长的细线一端固定在带有遮光片(宽度为d)的滑块上,另一端通过光滑定滑轮与重物相连,细线与斜面平行(通过滑轮调节).当滑块沿斜面下滑时,与光电门相连的计时器可以显示遮光片挡光的时间t,从而可测出滑块通过光电门时的瞬时速度v.改变光电门甲的位置,重复实验,比较外力所做的功W与系统动能的增量△Ek的关系,即可达到实验目的.
现要用如图所示的实验装置探究“动能定理”:一倾角θ可调的斜面上安装有两个光电门,其中光电门乙固定在斜面上,光电门甲的位置可移动.不可伸长的细线一端固定在带有遮光片(宽度为d)的滑块上,另一端通过光滑定滑轮与重物相连,细线与斜面平行(通过滑轮调节).当滑块沿斜面下滑时,与光电门相连的计时器可以显示遮光片挡光的时间t,从而可测出滑块通过光电门时的瞬时速度v.改变光电门甲的位置,重复实验,比较外力所做的功W与系统动能的增量△Ek的关系,即可达到实验目的.