题目内容
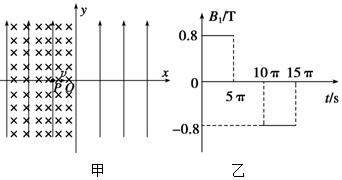
3. 如图所示,光滑水平面上有一矩形长木板,木板左端放一小物块,已知木板质量大于物块质量,t=0时两者从图中位置以相同的水平速度v0向右运动,碰到右面的竖直挡板后木板以与原来等大反向的速度被反弹回来,运动过程中物块一直未离开木板,则关于物块运动的速度v随时间t变化的图象可能正确的是( )
如图所示,光滑水平面上有一矩形长木板,木板左端放一小物块,已知木板质量大于物块质量,t=0时两者从图中位置以相同的水平速度v0向右运动,碰到右面的竖直挡板后木板以与原来等大反向的速度被反弹回来,运动过程中物块一直未离开木板,则关于物块运动的速度v随时间t变化的图象可能正确的是( )| A. |  | B. |  | C. |  | D. |  |
分析 木板碰到挡板前,物块与木板一直做匀速运动,木板碰到挡板后,物块继续向右做匀减速运动,木板向左做匀减速运动,最终两者速度相同,由动量守恒分析最终的速度,即可选择图象.
解答 解:木板碰到挡板前,物块与木板一直做匀速运动,速度为v0;木板碰到挡板后,物块向右做匀减速运动,速度减至零后向左做匀加速运动,木板向左做匀减速运动,最终两者速度相同,设为v.
设木板的质量为M,物块的质量为m,取向左为正方向,则由动量守恒得:Mv0-mv0=(M+m)v,得 v=$\frac{M-m}{M+m}{v}_{0}$<v0
故A正确,BCD错误.
故选:A.
点评 解决本题的关键要正确分析物体的运动情况,明确木板碰到挡板后,系统的动量守恒,运用动量守恒定律研究最终的共同速度.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
14. 如图所示,表面粗糙、倾角为θ的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过滑轮.初始时刻,A、B处于静止状态且B不受摩擦力.现施加一沿斜面向下的恒力F,使B沿斜面下滑,当质量为m的A物块上升h高度的过程中(不计滑轮的质量和摩擦)( )
如图所示,表面粗糙、倾角为θ的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过滑轮.初始时刻,A、B处于静止状态且B不受摩擦力.现施加一沿斜面向下的恒力F,使B沿斜面下滑,当质量为m的A物块上升h高度的过程中(不计滑轮的质量和摩擦)( )
 如图所示,表面粗糙、倾角为θ的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过滑轮.初始时刻,A、B处于静止状态且B不受摩擦力.现施加一沿斜面向下的恒力F,使B沿斜面下滑,当质量为m的A物块上升h高度的过程中(不计滑轮的质量和摩擦)( )
如图所示,表面粗糙、倾角为θ的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过滑轮.初始时刻,A、B处于静止状态且B不受摩擦力.现施加一沿斜面向下的恒力F,使B沿斜面下滑,当质量为m的A物块上升h高度的过程中(不计滑轮的质量和摩擦)( )| A. | A、B组成的系统机械能守恒 | B. | A、B组成的系统机械能增加Fh | ||
| C. | A、B组成的系统动能增加Fh | D. | 物块B重力势能减少mgh |
11. 如图,甲、乙两物体用压缩的轻质弹簧连接静置于倾角为θ的粗糙斜面体上.斜面体始终保持静止,则下列判断正确的是( )
如图,甲、乙两物体用压缩的轻质弹簧连接静置于倾角为θ的粗糙斜面体上.斜面体始终保持静止,则下列判断正确的是( )
 如图,甲、乙两物体用压缩的轻质弹簧连接静置于倾角为θ的粗糙斜面体上.斜面体始终保持静止,则下列判断正确的是( )
如图,甲、乙两物体用压缩的轻质弹簧连接静置于倾角为θ的粗糙斜面体上.斜面体始终保持静止,则下列判断正确的是( )| A. | 物体甲所受的摩擦力可能为零 | B. | 物体甲一定受到四个力作用 | ||
| C. | 物体乙所受的摩擦力可能为零 | D. | 水平面对斜面体无摩擦力作用 |
15.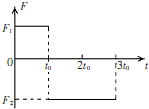 一静止的物体所受到的合外力随时间的变化关系如图所示,图中F1、F2未知.已知物体从t=0时刻出发,在3t0时刻恰又返回到出发点,则( )
一静止的物体所受到的合外力随时间的变化关系如图所示,图中F1、F2未知.已知物体从t=0时刻出发,在3t0时刻恰又返回到出发点,则( )
 一静止的物体所受到的合外力随时间的变化关系如图所示,图中F1、F2未知.已知物体从t=0时刻出发,在3t0时刻恰又返回到出发点,则( )
一静止的物体所受到的合外力随时间的变化关系如图所示,图中F1、F2未知.已知物体从t=0时刻出发,在3t0时刻恰又返回到出发点,则( )| A. | O~to物体做匀加速直线运动,to-3to物体做匀减速直线运动 | |
| B. | 物体在F1作用下的位移与在F2作用下的位移相等 | |
| C. | t0时刻物体的速度与3t0时刻物体的速度大小之比为$\frac{2}{3}$ | |
| D. | F1与F2大小之比为$\frac{6}{5}$ |
4.关于物理学发展,下列表述不正确的有( )
| A. | 伽利略通过斜面实验得出自由落体运动位移与时间的平方成正比 | |
| B. | 安培通过实验研究,发现了电流周围存在磁场 | |
| C. | 笛卡儿明确指出:除非物体受到力的作用,物体将永远保持其静止或运动状态,永远不会使自己沿曲线运动,而只保持在直线上运动 | |
| D. | 伽利略科学思想方法的核心是把实验和逻辑推理和谐地结合起来,从而有力地推进了人类科学认识的发展 |
 如图所示,水平平台ab长为20m,平台b端与长度未知的特殊材料制成的斜面bc连接,斜面倾角为30°.在平台b端放上质量为5kg的物块,并给物块施加与水平方向成37°角的50N推力后,物块由静止开始运动.己知物块与平台间的动摩擦因数为0.4,重力加速度g=10m/s2,sin37°=0.6,求:(第(2)、(3)两问结果保留三位有效数字)
如图所示,水平平台ab长为20m,平台b端与长度未知的特殊材料制成的斜面bc连接,斜面倾角为30°.在平台b端放上质量为5kg的物块,并给物块施加与水平方向成37°角的50N推力后,物块由静止开始运动.己知物块与平台间的动摩擦因数为0.4,重力加速度g=10m/s2,sin37°=0.6,求:(第(2)、(3)两问结果保留三位有效数字)