题目内容
17.地球半径为R,地面附近的重力加速度为g,试求在离地面高度为R处的重力加速度及质量为m的物体在这一高度的引力大小.若离地面高度为H时,重力加速度又是多少?分析 由地面的万有引力等于重力,再列高空的万有引力等于重力,联合可得高空重力加速度表达式.
解答 解:地面万有引力等于重力:$G\frac{Mm}{{R}^{2}}=mg$,
在离地面高度为R处:$G\frac{Mm}{({R+R)}^{2}}=m{g}_{1}$
解得:${g}_{1}=({\frac{1}{2})}^{2}g=\frac{g}{4}$
故引力为F=mg1=$\frac{mg}{4}$
离地面高度为H时,$G\frac{Mm}{{(R+H)}^{2}}=m{g}_{2}$
解得${g}_{2}=(\frac{R}{R+H})^{2}g$
答:在离地面高度为R处的重力加速度为$\frac{g}{4}$,质量为m的物体在这一高度的引力大小为$\frac{mg}{4}$.
若离地面高度为H时,重力加速度为${(\frac{R}{R+H})}^{2}g$.
点评 本题考查万有引力的应用,要能根据公式求解重力加速度.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
8. 如图所示,弹簧下端悬一滑轮,跨过滑轮的细线两端系有A、B两重物,mB=2kg,不计线、滑轮质量及摩擦,将A、B两重物由静止释放后,弹簧的示数不可能为:(g=10m/s2)( )
如图所示,弹簧下端悬一滑轮,跨过滑轮的细线两端系有A、B两重物,mB=2kg,不计线、滑轮质量及摩擦,将A、B两重物由静止释放后,弹簧的示数不可能为:(g=10m/s2)( )
 如图所示,弹簧下端悬一滑轮,跨过滑轮的细线两端系有A、B两重物,mB=2kg,不计线、滑轮质量及摩擦,将A、B两重物由静止释放后,弹簧的示数不可能为:(g=10m/s2)( )
如图所示,弹簧下端悬一滑轮,跨过滑轮的细线两端系有A、B两重物,mB=2kg,不计线、滑轮质量及摩擦,将A、B两重物由静止释放后,弹簧的示数不可能为:(g=10m/s2)( )| A. | 40N | B. | 60N | C. | 70N | D. | 100N |
12. 如图所示,一名消防队员在模拟演习训练中,沿着长为12m的竖立在地面上的钢管往下滑.已知这名消防队员的质量为60㎏,他从钢管顶端由静止开始先匀加速再匀减速下滑,滑到地面时速度恰好为零.如果他加速时的加速度大小是减速时的2倍,下滑的总时间为3s,g取10m/s2,那么该消防队员( )
如图所示,一名消防队员在模拟演习训练中,沿着长为12m的竖立在地面上的钢管往下滑.已知这名消防队员的质量为60㎏,他从钢管顶端由静止开始先匀加速再匀减速下滑,滑到地面时速度恰好为零.如果他加速时的加速度大小是减速时的2倍,下滑的总时间为3s,g取10m/s2,那么该消防队员( )
 如图所示,一名消防队员在模拟演习训练中,沿着长为12m的竖立在地面上的钢管往下滑.已知这名消防队员的质量为60㎏,他从钢管顶端由静止开始先匀加速再匀减速下滑,滑到地面时速度恰好为零.如果他加速时的加速度大小是减速时的2倍,下滑的总时间为3s,g取10m/s2,那么该消防队员( )
如图所示,一名消防队员在模拟演习训练中,沿着长为12m的竖立在地面上的钢管往下滑.已知这名消防队员的质量为60㎏,他从钢管顶端由静止开始先匀加速再匀减速下滑,滑到地面时速度恰好为零.如果他加速时的加速度大小是减速时的2倍,下滑的总时间为3s,g取10m/s2,那么该消防队员( )| A. | 下滑过程中的最大速度为4 m/s | |
| B. | 加速与减速过程的时间之比为1:2 | |
| C. | 加速与减速过程中所受钢管弹力大小之比为1:7 | |
| D. | 加速与减速过程的位移之比为1:4 |
2. 带等量的同种正电的点电荷的连线和中垂线如图20所示.现将一个带负电的试探电荷先从图中a点沿直线移到b点,再从b点沿直线移到c点,则试探电荷在这全过程中一定有( )
带等量的同种正电的点电荷的连线和中垂线如图20所示.现将一个带负电的试探电荷先从图中a点沿直线移到b点,再从b点沿直线移到c点,则试探电荷在这全过程中一定有( )
 带等量的同种正电的点电荷的连线和中垂线如图20所示.现将一个带负电的试探电荷先从图中a点沿直线移到b点,再从b点沿直线移到c点,则试探电荷在这全过程中一定有( )
带等量的同种正电的点电荷的连线和中垂线如图20所示.现将一个带负电的试探电荷先从图中a点沿直线移到b点,再从b点沿直线移到c点,则试探电荷在这全过程中一定有( )| A. | 所受的电场力先减小后增大 | |
| B. | 所受的电场力先做负功后做正功 | |
| C. | 电势能一直减小 | |
| D. | 两正电荷在a、b、c三点产生的电势高低情况为:φa<φb<φc |
 一质量为m的滑块(视为质点),从水平面上与一平面相切与A点以V0=$\sqrt{8Rg}$的速度进入竖直半圆形轨道开始作圆周运动,轨道半径为R,经半圆轨道的最高点B飞出,落回到水平面上的C点,如图所示,若AC=2AB=4R
一质量为m的滑块(视为质点),从水平面上与一平面相切与A点以V0=$\sqrt{8Rg}$的速度进入竖直半圆形轨道开始作圆周运动,轨道半径为R,经半圆轨道的最高点B飞出,落回到水平面上的C点,如图所示,若AC=2AB=4R 如图所示,在竖直平面内,粗糙的斜面轨道AB的下端与光滑的圆弧轨道BCD相切于B点,C是最低点,圆心角∠BOC=37°,D与圆心O等高,圆弧轨道半径R=1.0m,现有一个质量为m=0.2kg可视为质点的小物体,从D点的正上方E点处自由下落,DE距离h=1.6m,物体与斜面AB之间的动摩擦因数μ=0.5.取sin37°=0.6,cos37°=0.8,g=10m/s2.求:
如图所示,在竖直平面内,粗糙的斜面轨道AB的下端与光滑的圆弧轨道BCD相切于B点,C是最低点,圆心角∠BOC=37°,D与圆心O等高,圆弧轨道半径R=1.0m,现有一个质量为m=0.2kg可视为质点的小物体,从D点的正上方E点处自由下落,DE距离h=1.6m,物体与斜面AB之间的动摩擦因数μ=0.5.取sin37°=0.6,cos37°=0.8,g=10m/s2.求: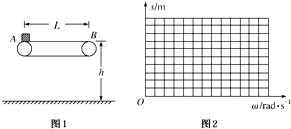 如图1所示为车站使用的水平传送带的模型,它的水平传送带AB的长度为L=8m,传送带的皮带轮的半径均为R=0.2m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(可视为质点)以初速度v0=10m/s水平地滑上水平传送带A端.已知旅行包与传送带之间的动摩擦因数为μ=0.6,皮带轮与皮带之间始终不打滑,g取10m/s2.讨论下列问题:
如图1所示为车站使用的水平传送带的模型,它的水平传送带AB的长度为L=8m,传送带的皮带轮的半径均为R=0.2m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(可视为质点)以初速度v0=10m/s水平地滑上水平传送带A端.已知旅行包与传送带之间的动摩擦因数为μ=0.6,皮带轮与皮带之间始终不打滑,g取10m/s2.讨论下列问题: 如图所示,传送带保持2m/s的速度顺时针转动.现将一质量m=0.5kg的物体轻轻地放在传送带的a点上,设物体与传送带间的动摩擦因数μ=0.2,a、b间的距离L=3m,则物体从a点运动到b点所经历的时间为 (g取10m/s2)( )
如图所示,传送带保持2m/s的速度顺时针转动.现将一质量m=0.5kg的物体轻轻地放在传送带的a点上,设物体与传送带间的动摩擦因数μ=0.2,a、b间的距离L=3m,则物体从a点运动到b点所经历的时间为 (g取10m/s2)( )