题目内容
11. 一质量为m的滑块(视为质点),从水平面上与一平面相切与A点以V0=$\sqrt{8Rg}$的速度进入竖直半圆形轨道开始作圆周运动,轨道半径为R,经半圆轨道的最高点B飞出,落回到水平面上的C点,如图所示,若AC=2AB=4R
一质量为m的滑块(视为质点),从水平面上与一平面相切与A点以V0=$\sqrt{8Rg}$的速度进入竖直半圆形轨道开始作圆周运动,轨道半径为R,经半圆轨道的最高点B飞出,落回到水平面上的C点,如图所示,若AC=2AB=4R求(1)B点的速度是多少?
(2)物体B点对轨道的压力是多少?
(3)物体A点对轨道的压力是多少?
分析 (1)物体C到A的过程中做平抛运动,将运动进行分解,根据平抛运动的规律求解滑块通过C点时的速度大小;
(2、3)在A点和B对物块进行受力分析,由牛顿第二定律求出滑块在A、B点受到的轨道的支持力,然后依据牛顿第三定律,即可得到滑块在B点对轨道的压力;
解答 解:(1)设滑块从B点飞出时的速度为vB,从B点运动到C点时间为t,滑块从B点飞出后,做平抛运动
竖直方向:2R=$\frac{1}{2}$gt2
水平方向:4R=vBt
解得:vB=$\sqrt{4Rg}$,
(2)设滑块在B点受轨道的支持力为FN,根据牛顿第二定律
FN+mg=m$\frac{{{v}_{B}}^{2}}{R}$
解得:FN=3mg
(3)设滑块在A点受轨道的支持力为FN′,根据牛顿第二定律
FN′-mg=m$\frac{{{v}_{0}}^{2}}{R}$
解得:FN′=9mg
答:(1)B点的速度是$\sqrt{4Rg}$
(2)物体B点对轨道的压力是3mg;
(3)物体A点对轨道的压力是9mg.
点评 本题是平抛运动与圆周运动相结合的题目,知道物体做圆周运动的向心力的来源,难度适中.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
1.质量为m的物体以初速度v0水平抛出,忽略空气阻力,物体在空中运动一段时间后,物体速度为v且与水平方向夹角为θ、重力加速度为g,此时物体重力的瞬时功率为( )
| A. | mgv0cosθ | B. | mgv0sinθ | C. | mgv | D. | mgvsinθ |
19. 质点S在竖直方向做简谐运动,形成简谐横波水平向右传播,P、Q是波上两点,如图所示,从质点S起振开始计时,当S第5次到达上方振幅位置时,质点P刚开始向下起振.已知SP=1.9m,SQ=2.5m,质点S做简谐运动的频率为100Hz,振幅为0.2m,以质点S所在位置为坐标原点,SP方向为x轴,建立直角坐标,则( )
质点S在竖直方向做简谐运动,形成简谐横波水平向右传播,P、Q是波上两点,如图所示,从质点S起振开始计时,当S第5次到达上方振幅位置时,质点P刚开始向下起振.已知SP=1.9m,SQ=2.5m,质点S做简谐运动的频率为100Hz,振幅为0.2m,以质点S所在位置为坐标原点,SP方向为x轴,建立直角坐标,则( )
 质点S在竖直方向做简谐运动,形成简谐横波水平向右传播,P、Q是波上两点,如图所示,从质点S起振开始计时,当S第5次到达上方振幅位置时,质点P刚开始向下起振.已知SP=1.9m,SQ=2.5m,质点S做简谐运动的频率为100Hz,振幅为0.2m,以质点S所在位置为坐标原点,SP方向为x轴,建立直角坐标,则( )
质点S在竖直方向做简谐运动,形成简谐横波水平向右传播,P、Q是波上两点,如图所示,从质点S起振开始计时,当S第5次到达上方振幅位置时,质点P刚开始向下起振.已知SP=1.9m,SQ=2.5m,质点S做简谐运动的频率为100Hz,振幅为0.2m,以质点S所在位置为坐标原点,SP方向为x轴,建立直角坐标,则( )| A. | 该波的传播速度为38m/s | |
| B. | 该波的波长为0.5m | |
| C. | 在t=0.08s时,质点Q已经运动的路程为1.4m | |
| D. | 在t=0.08s时,质点P、Q之间2.1m<x<2.3m的质点向下 |
 如图为一种延时继电器的示意图,铁芯上有两个线圈A和B,线圈A和电源连接,线圈B两端连在一起,构成一个闭合电路.在断开开关S的时候,弹簧E并不会立刻将衔铁D拉起而使接触头C(连接工作电路)离开,而是过一小段时间后才执行这个动作.线圈B若不闭合,影响(填“影响”或“不影响”)延时效果,原因是线圈B不闭合,则不会产生感应电流,不会有此效果.
如图为一种延时继电器的示意图,铁芯上有两个线圈A和B,线圈A和电源连接,线圈B两端连在一起,构成一个闭合电路.在断开开关S的时候,弹簧E并不会立刻将衔铁D拉起而使接触头C(连接工作电路)离开,而是过一小段时间后才执行这个动作.线圈B若不闭合,影响(填“影响”或“不影响”)延时效果,原因是线圈B不闭合,则不会产生感应电流,不会有此效果. 一列沿x轴传播的间谐横波在t=0时刻的波的图象如图所示,经△t=0.1s,质点M第一次回到平衡位置,求:
一列沿x轴传播的间谐横波在t=0时刻的波的图象如图所示,经△t=0.1s,质点M第一次回到平衡位置,求: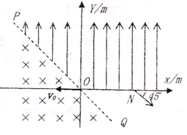 如图所示,在xoy平面内,直线PQ平分第二、四象限(即与y轴成45°),直线PQ左侧空间存在着垂直纸面向里的匀强磁场,PQ上侧且y>0空间存在着沿y轴正方向的匀强电场,场强大小为E=10V/m;一个比荷$\frac{q}{m}$=103C/kg的带负电的粒子(重力不计),从坐标原点O以v0=200m/s的速度沿着x轴负方向进入匀强磁场,粒子从O点入射后,最后从x轴上N点射出电场,方向恰好与x轴正方向成45°,求:
如图所示,在xoy平面内,直线PQ平分第二、四象限(即与y轴成45°),直线PQ左侧空间存在着垂直纸面向里的匀强磁场,PQ上侧且y>0空间存在着沿y轴正方向的匀强电场,场强大小为E=10V/m;一个比荷$\frac{q}{m}$=103C/kg的带负电的粒子(重力不计),从坐标原点O以v0=200m/s的速度沿着x轴负方向进入匀强磁场,粒子从O点入射后,最后从x轴上N点射出电场,方向恰好与x轴正方向成45°,求: