题目内容
9.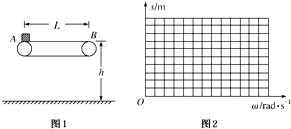 如图1所示为车站使用的水平传送带的模型,它的水平传送带AB的长度为L=8m,传送带的皮带轮的半径均为R=0.2m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(可视为质点)以初速度v0=10m/s水平地滑上水平传送带A端.已知旅行包与传送带之间的动摩擦因数为μ=0.6,皮带轮与皮带之间始终不打滑,g取10m/s2.讨论下列问题:
如图1所示为车站使用的水平传送带的模型,它的水平传送带AB的长度为L=8m,传送带的皮带轮的半径均为R=0.2m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(可视为质点)以初速度v0=10m/s水平地滑上水平传送带A端.已知旅行包与传送带之间的动摩擦因数为μ=0.6,皮带轮与皮带之间始终不打滑,g取10m/s2.讨论下列问题:(1)若传送带静止,旅行包滑到B点时,人若没有及时取下,旅行包将从B端滑落,则包的落地点距B端的水平距离为多少?
(2)设皮带轮顺时针匀速运动,若皮带轮的角速度ω1=40rad/s,旅行包落地点距B端的水平距离又为多少?
分析 (1)根据牛顿第二定律求出旅行包做匀减速直线运动的加速度大小,根据速度位移公式求出旅行包到达B端的速度,离开B点做平抛运动,根据高度求出平抛运动的时间,从而求出水平位移.
(2)若皮带轮的角速度ω1=40rad/s,根据v=Rω求出皮带线速度的大小,得知旅行包滑上传送带做匀减速直线运动,当速度达到传送带速度做匀速直线运动.从而根据平抛运动知识求出旅行包落地点距B端的水平距离.
解答 解:(1)从A到B过程中,旅行包做匀减速运动,根据牛顿第二定律,有:
ma=μmg
解得:a=6 m/s2
旅行包到达B端的速度为:
v=$\sqrt{v_0^2-2aL}=\sqrt{100-96}$m/s=2 m/s
包的落地点距B端的水平距离为:
s=vt=v$\sqrt{\frac{2h}{g}}$=2×$\sqrt{\frac{2×0.45}{10}}$m=0.6 m
(2)当ω1=40 rad/s,皮带速度为:v1=ω1R=8 m/s,
当旅行包的速度也为v1=8 m/s时,在传送带上运动了位移:
s1=$\frac{{v}_{0}^{2}-{v}_{1}^{2}}{2a}$=$\frac{100-64}{2×6}$m=3 m<8 m
以后旅行包做匀速直线运动,所以旅行包到达B点的速度也为:v1=8 m/s,
包的落地点距B端的水平距离为:
s2=v1t=v1$\sqrt{\frac{2h}{g}}$=8×2×$\sqrt{\frac{2×0.45}{10}}$m=2.4 m
答:(1)包的落地点距B端的水平距离为0.6m;
(2)旅行包落地点距B端的水平距离为2.4m.
点评 解决本题的关键通过传送带的速度,根据旅行包的受力判断出运动规律,根据牛顿第二定律和运动学公式进行求解.

练习册系列答案
相关题目
20. 如图所示,虚线表示某点电荷Q所激发电场的等势面,已知a、b两点在同一等势面上,c、d两点在另一个等势面上.甲、乙两个带电粒子以相同的速率,沿不同的方向从同一点a射入电场,在电场中沿不同的轨迹adb曲线、acb曲线运动.则下列说法正确的是( )
如图所示,虚线表示某点电荷Q所激发电场的等势面,已知a、b两点在同一等势面上,c、d两点在另一个等势面上.甲、乙两个带电粒子以相同的速率,沿不同的方向从同一点a射入电场,在电场中沿不同的轨迹adb曲线、acb曲线运动.则下列说法正确的是( )
 如图所示,虚线表示某点电荷Q所激发电场的等势面,已知a、b两点在同一等势面上,c、d两点在另一个等势面上.甲、乙两个带电粒子以相同的速率,沿不同的方向从同一点a射入电场,在电场中沿不同的轨迹adb曲线、acb曲线运动.则下列说法正确的是( )
如图所示,虚线表示某点电荷Q所激发电场的等势面,已知a、b两点在同一等势面上,c、d两点在另一个等势面上.甲、乙两个带电粒子以相同的速率,沿不同的方向从同一点a射入电场,在电场中沿不同的轨迹adb曲线、acb曲线运动.则下列说法正确的是( )| A. | 两粒子所带的电荷符号可能相同 | |
| B. | 甲粒子经过c点时的速度大于乙粒子经过d点的速度 | |
| C. | 两个粒子的电势能都是先减小后增大 | |
| D. | 经过b点时,两粒子的动能一定相等 |
4. 如图所示,两根细线把两个相同的小球悬于同一点,并使两球在同一水平面内做匀速圆周运动,其中小球1的转动半径较大,则( )
如图所示,两根细线把两个相同的小球悬于同一点,并使两球在同一水平面内做匀速圆周运动,其中小球1的转动半径较大,则( )
 如图所示,两根细线把两个相同的小球悬于同一点,并使两球在同一水平面内做匀速圆周运动,其中小球1的转动半径较大,则( )
如图所示,两根细线把两个相同的小球悬于同一点,并使两球在同一水平面内做匀速圆周运动,其中小球1的转动半径较大,则( )| A. | 两小球转动的加速速度大小关系为a1>a2 | |
| B. | 两小球转动的角速度大小关系为ω1=ω2 | |
| C. | 两小球转动的线速度大小关系为v1=v2 | |
| D. | 两根线中拉力大小关系为T1>T2 |
14.下列物理量属于矢量的是( )
| A. | 质量 | B. | 速率 | C. | 速度 | D. | 路程 |
1.下列说法中正确的是( )
| A. | 当一定气体吸热时,其内能可能减少 | |
| B. | 玻璃、石墨、金刚石都是晶体;木炭是非晶体 | |
| C. | 单晶体有固定的熔点,非晶体和多晶体没有固定的熔点 | |
| D. | 当液体和大气相接触时,液体表面层内的分子所受其它分子作用力的合力总是指向液体内部 | |
| E. | 气体分子单位时间内与单位面积器壁碰撞的次数,与单位体积内气体分子的总数和气体温度有关 |
18.如图是A、B两物体运动的速度图象,则下列说法正确的是( )


| A. | 物体A的运动是以10m/s的速度匀速运动 | |
| B. | 物体B的运动是以5m/s的速度与A同方向 | |
| C. | 物体B在最初3s内位移是10m | |
| D. | 物体B在最初3s内路程是10m |
19.(多选)如图所示为两个独立电路A和B的路端电压与其总电流I的关系图线,则( )


| A. | 路端电压都为U1时,它们的外电阻相等 | |
| B. | 电流都是I1时,两电源内电压相等 | |
| C. | 电路A的电动势小于电路B的电动势 | |
| D. | A中电源的内阻大于B中电源的内阻 |
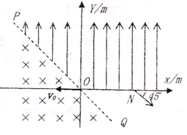 如图所示,在xoy平面内,直线PQ平分第二、四象限(即与y轴成45°),直线PQ左侧空间存在着垂直纸面向里的匀强磁场,PQ上侧且y>0空间存在着沿y轴正方向的匀强电场,场强大小为E=10V/m;一个比荷$\frac{q}{m}$=103C/kg的带负电的粒子(重力不计),从坐标原点O以v0=200m/s的速度沿着x轴负方向进入匀强磁场,粒子从O点入射后,最后从x轴上N点射出电场,方向恰好与x轴正方向成45°,求:
如图所示,在xoy平面内,直线PQ平分第二、四象限(即与y轴成45°),直线PQ左侧空间存在着垂直纸面向里的匀强磁场,PQ上侧且y>0空间存在着沿y轴正方向的匀强电场,场强大小为E=10V/m;一个比荷$\frac{q}{m}$=103C/kg的带负电的粒子(重力不计),从坐标原点O以v0=200m/s的速度沿着x轴负方向进入匀强磁场,粒子从O点入射后,最后从x轴上N点射出电场,方向恰好与x轴正方向成45°,求: