题目内容
14. 如图所示,一个质量为m=1kg的小球在高度为h=0.2m的弯曲轨道AB从最高点A点静止释放,最后离开B后做平抛运动,随后在C点恰好沿圆弧切线方向进入一个固定的光滑圆弧轨道CDE中,并且恰能通过圆弧的最高点E,已知圆弧半径R=0.3m,圆心O与C的连线OC与竖直方向的夹角θ=60°,取重力加速度g=10m/s2.试求:
如图所示,一个质量为m=1kg的小球在高度为h=0.2m的弯曲轨道AB从最高点A点静止释放,最后离开B后做平抛运动,随后在C点恰好沿圆弧切线方向进入一个固定的光滑圆弧轨道CDE中,并且恰能通过圆弧的最高点E,已知圆弧半径R=0.3m,圆心O与C的连线OC与竖直方向的夹角θ=60°,取重力加速度g=10m/s2.试求:(1)在圆弧切入点C时轨道对小球的作用力F1;
(2)在弯曲轨道AB中运动时阻力对小球做的功W1;
(3)B与E点的距离S.(结果保留两位有效数字)
分析 (1)根据牛顿第二定律求出最高点E的速度,结合动能定理求出C点的速度,根据牛顿第二定律,抓住径向的合力提供向心力求出在圆弧切入点C时轨道对小球的作用力;
(2)根据平行四边形定则求出平抛运动的初速度,对AB段运用动能定理,求出阻力做功的大小.
(3)根据平行四边形定则求出C点的竖直分速度,结合速度时间公式求出平抛运动的时间,从而得出平抛运动的水平位移和竖直位移,结合几何关系求出BE间的距离.
解答 解:(1)
 小球恰能通过圆弧的最高点E,
小球恰能通过圆弧的最高点E,
根据牛顿第二定律得,mg=$m\frac{{{v}_{E}}^{2}}{R}$,
解得${v}_{E}=\sqrt{gR}$=$\sqrt{10×0.3}$m/s=$\sqrt{3}$m/s,
根据动能定理得,$-mgR(1+cosθ)=\frac{1}{2}m{{v}_{E}}^{2}-\frac{1}{2}m{{v}_{C}}^{2}$,
代入数据解得vC=$2\sqrt{3}$m/s.
根据牛顿第二定律得,${F}_{1}-mgcos60°=m\frac{{{v}_{C}}^{2}}{R}$,
解得F1=45N.
(2)在C点,根据平行四边形定则知,${v}_{0}={v}_{C}cos60°=\sqrt{3}m/s$,
根据动能定理得,$mgh+{W}_{1}=\frac{1}{2}m{{v}_{0}}^{2}-0$,
代入数据解得W1=-0.5J.
(3)小球在C点的竖直分速度${v}_{y}={v}_{c}sin60°=2\sqrt{3}×\frac{\sqrt{3}}{2}m/s=3m/s$,
则B到C的时间$t=\frac{{v}_{y}}{g}=\frac{3}{10}s=0.3s$,
BC间的高度差$h′=\frac{1}{2}g{t}^{2}=\frac{1}{2}×10×0.09m=0.45m$,
则BD间的高度差$h″=h′+\frac{1}{2}R=0.45+0.15m=0.6m$,
DE的高度差为2R=0.6m,
则BE等高,
所以BE间的距离S=${v}_{0}t+Rsinθ=\sqrt{3}×0.3+0.3×\frac{\sqrt{3}}{2}$m=$0.45\sqrt{3}$m≈0.78m.
答:(1)在圆弧切入点C时轨道对小球的作用力F1为45N;
(2)在弯曲轨道AB中运动时阻力对小球做的功W1为-0.5J;
(3)B与E点的距离S为0.78m.
点评 本题是平抛运动和圆周运动相结合的典型题目,除了运用平抛运动和圆周运动的基本公式外,求速度的问题,动能定理不失为一种好的方法.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案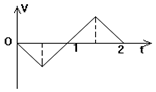
| A. | t=0.5 s时离原点最远 | B. | t=1 s时离原点最远 | ||
| C. | t=1 s时回到原点 | D. | t=2 s时回到原点 |
 如图所示,一匝数为10匝的矩形线圈全部处在磁场中,现匀速向右拉出磁场.在此过程中,线圈的磁通量将变小 (选填“变大”、“变小”或“不变”).若上述过程所经历的时间为0.2s,线圈中产生的感应电动势为2V,则线圈中的磁通量变化了0.04Wb.
如图所示,一匝数为10匝的矩形线圈全部处在磁场中,现匀速向右拉出磁场.在此过程中,线圈的磁通量将变小 (选填“变大”、“变小”或“不变”).若上述过程所经历的时间为0.2s,线圈中产生的感应电动势为2V,则线圈中的磁通量变化了0.04Wb. 风洞实验室中可产生方向、大小都可以调节控制的各种风力,如图所示为某风洞里模拟做实验的示意图.一质量为m=1.0kg的小球套在一根固定的足够长直杆上,直杆与水平面夹角为30°.现小球在F=16N的竖直向上的风力作用下,从A点由静止出发沿直杆向上运动,已知杆的摩擦忽略不计,重力加速度g取10m/s,试求:
风洞实验室中可产生方向、大小都可以调节控制的各种风力,如图所示为某风洞里模拟做实验的示意图.一质量为m=1.0kg的小球套在一根固定的足够长直杆上,直杆与水平面夹角为30°.现小球在F=16N的竖直向上的风力作用下,从A点由静止出发沿直杆向上运动,已知杆的摩擦忽略不计,重力加速度g取10m/s,试求: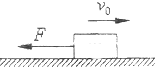 如图所示,质量为m=1kg,初速度为v0=10m/s的物体沿粗糙水平面滑动,物体与地面间的动摩擦因数μ=0.2;同时还受一个与运动方向相反、大小为F=3N的水平外力作用,经3s后撤去外力,求:物体能滑行的总位移X.
如图所示,质量为m=1kg,初速度为v0=10m/s的物体沿粗糙水平面滑动,物体与地面间的动摩擦因数μ=0.2;同时还受一个与运动方向相反、大小为F=3N的水平外力作用,经3s后撤去外力,求:物体能滑行的总位移X.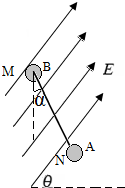 如图所示,整个装置处于真空中.一根长L=1.5m的光滑绝缘细直杆MN,与竖直方向成α=30°固定在场强大小为E=1.0×105N/C、与水平方向成θ=60°角的倾斜向上匀强电场中.杆的下端N固定一个带电小球A,电荷量Q=+4.5×10-6C;另一带电小球B穿在杆上可自由滑动,电荷量q=+1.0×10-6C,质量m=1.0×10-2kg.已知真空中点电荷q周围的电势ϕ=k$\frac{q}{r}$(取无穷远处为零电势,k=9.0×109N•m2/C2).现将小球B从杆的上端M静止释放,小球B开始运动.求:(重力加速度g=10m/s2)
如图所示,整个装置处于真空中.一根长L=1.5m的光滑绝缘细直杆MN,与竖直方向成α=30°固定在场强大小为E=1.0×105N/C、与水平方向成θ=60°角的倾斜向上匀强电场中.杆的下端N固定一个带电小球A,电荷量Q=+4.5×10-6C;另一带电小球B穿在杆上可自由滑动,电荷量q=+1.0×10-6C,质量m=1.0×10-2kg.已知真空中点电荷q周围的电势ϕ=k$\frac{q}{r}$(取无穷远处为零电势,k=9.0×109N•m2/C2).现将小球B从杆的上端M静止释放,小球B开始运动.求:(重力加速度g=10m/s2) 图甲为《探究电磁感应现象》实验中所用器材的示意图.现将电池组、滑动变阻器、带铁芯的线圈A、B,电流计及开关连接成如图甲所示的电路.
图甲为《探究电磁感应现象》实验中所用器材的示意图.现将电池组、滑动变阻器、带铁芯的线圈A、B,电流计及开关连接成如图甲所示的电路.