题目内容
5. 如图所示,左侧为板长L=0.1m、板间距d=$\frac{\sqrt{3}}{30}$m的平行金属板,加上U=
如图所示,左侧为板长L=0.1m、板间距d=$\frac{\sqrt{3}}{30}$m的平行金属板,加上U=$\frac{1}{3}$×104V 的电压,上极板电势高.现从平行金属板左端沿中心轴线方向射入一个重力不计的带电微粒,微粒质量m=1.0×10-10kg,带电荷量q=+1.0×10-4C,初速度v0=1.0×105m/s.右侧用虚线框表示的正三角形区域内存在垂直纸面向里的匀强磁场,三角形的顶点A与上金属板平齐,底边BC与金属板平行且距A足够远,下金属板的右端点P 恰在AB边上.
(1)求带电微粒从电场中射出时,竖直方向的偏移量y的大小;
(2)带电微粒进入三角形区域后,若垂直AC边射出,则该区域的磁感应强度B是多少.
分析 (1)根据带电粒子在水平方向的匀速直线运动求解时间,再根据竖直方向的匀加速直线运动时间竖直方向偏转的位移;
(2)求出粒子进入磁场时的速度大小和方向,再根据几何关系求解半径,根据洛伦兹力提供向心力求解磁感应强度B.
解答 解:(1)设微粒在电场中做类平抛运动的时间为t,加速度为a,射出电场时竖直方向的速度为vy,
则可得$\frac{qU}{d}$=ma
水平方向有:L=v0t
设带电微粒射出电场时竖直方向偏转的位移为y,则有y=$\frac{1}{2}$at2
可得y=$\frac{\sqrt{3}}{60}$ m;
(2)竖直方向,根据速度时间关系可得:vy=at
解得vy=$\frac{\sqrt{3}}{3}$×105 m/s
v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\frac{2\sqrt{3}}{3}$×105 m/s,
设速度v与水平方向的夹角为θ,则有tan θ=$\frac{{v}_{y}}{{v}_{0}}$=$\frac{\sqrt{3}}{3}$
即垂直于AB射出.即微粒由P1点垂直AB射入磁场
设匀速圆周运动P1Q1段半径为R1,根据几何关系有R1=$\frac{d}{cos30°}$=$\frac{20}{3}$×10-2m
由qvB1=m$\frac{{v}^{2}}{{R}_{1}}$
得B1=$\frac{mv}{q{B}_{2}}$=$\sqrt{3}$T.
答:(1)求带电微粒从电场中射出时,竖直方向的偏移量y的大小为$\frac{\sqrt{3}}{60}$ m;
(2)带电微粒进入三角形区域后,若垂直AC边射出,则该区域的磁感应强度B是$\sqrt{3}$T.
点评 对于带电粒子在磁场中的运动情况分析,一般是确定圆心位置,根据几何关系求半径,结合洛伦兹力提供向心力求解未知量;根据周期公式结合轨迹对应的圆心角求时间;对于带电粒子在电场中运动时,一般是按类平抛运动的知识进行解答.

 研究表明,两个邻近的分子之间同时存在着引力和斥力,如图中虚线所示,分子间作用力的合力随分子间距变化的关系如图中实线所示.关于分子间的作用力和分子势能,下列说法正确的是( )
研究表明,两个邻近的分子之间同时存在着引力和斥力,如图中虚线所示,分子间作用力的合力随分子间距变化的关系如图中实线所示.关于分子间的作用力和分子势能,下列说法正确的是( )| A. | 分子间距增大,斥力减小,引力增大 | |
| B. | 由图可知,当分子间的距离为r0时分子间作用力合力为0 | |
| C. | 当分子间的距离r<r0时,减小分子间距离,分子间作用力做负功,分子势能增加 | |
| D. | 当分子间的距离r>r0时,增大分子间距离,分子间作用力做正功,分子势能减少 |
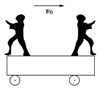 如图所示,光滑平面上有一辆质量为4m的小车,车上左右两端分别站着甲、乙两人,他们的质量都是m,开始两个人和车一起以速度v0向右匀速运动.某一时刻,站在车右端的乙先以相对地面向右的速度v跳离小车,然后站在车左端的甲以相对于地面向左的速度v跳离小车.两人都离开小车后,小车的速度将是( )
如图所示,光滑平面上有一辆质量为4m的小车,车上左右两端分别站着甲、乙两人,他们的质量都是m,开始两个人和车一起以速度v0向右匀速运动.某一时刻,站在车右端的乙先以相对地面向右的速度v跳离小车,然后站在车左端的甲以相对于地面向左的速度v跳离小车.两人都离开小车后,小车的速度将是( )| A. | 1.5v0 | B. | v0 | ||
| C. | 大于v0,小于1.5v0 | D. | 大于1.5v0 |
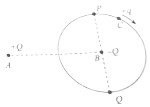
| A. | 电荷C的运动轨迹上各点的电势均为负值 | |
| B. | 电荷C顺时针运动,则从P到Q的运动过程中,电势能先增打后减小 | |
| C. | 电荷C运动一周,外力F做功为零 | |
| D. | 若电荷C绕A做同样的运动,与绕B的运动相比,在对应位置需要的外力F大小相等,方向相反 |
 如图所示,Q1、Q2为真空中的两等量异种点电荷,Q1带正电,Q2带负电,两点电荷的连线沿水平方向,有一根足够长的光滑绝缘杆位于两电荷连线的正上方,且与连线平行,一带负电的圆环A穿在光滑的杆上,圆环的半径略大于杆,给圆环一初速度,使其自左向右依次通过a、b、c三点,已知ab=bc,且b点位于Q1、Q2连线的中垂线上,a,c两点离电荷Q1,Q2较远,则下列说法正确的是( )
如图所示,Q1、Q2为真空中的两等量异种点电荷,Q1带正电,Q2带负电,两点电荷的连线沿水平方向,有一根足够长的光滑绝缘杆位于两电荷连线的正上方,且与连线平行,一带负电的圆环A穿在光滑的杆上,圆环的半径略大于杆,给圆环一初速度,使其自左向右依次通过a、b、c三点,已知ab=bc,且b点位于Q1、Q2连线的中垂线上,a,c两点离电荷Q1,Q2较远,则下列说法正确的是( )| A. | 当圆环位于b点的左侧时,杆对环的弹力方向先是竖直向上后是竖直向下的 | |
| B. | 圆环从a运动至b的过程中,速度先增大后减小 | |
| C. | 圆环经过b点时的动能最小 | |
| D. | 圆环在a点的电势能大于在c点的电势能 |
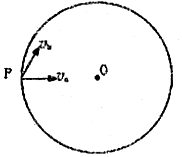 如图所示,圆心区域内有垂直纸面的匀强磁场(图中未画出),O为圆心,P为边界上的一点,相同的带负电粒子a、b(不计重力)从P点先后射入磁场,粒子a正对圆心射入,速度方向改变60°后离开磁场,粒子b射入磁场时的速度方向与粒子a射入时的速度方向成60°,已知它们离开磁场的位置相同,下列说法正确的是( )
如图所示,圆心区域内有垂直纸面的匀强磁场(图中未画出),O为圆心,P为边界上的一点,相同的带负电粒子a、b(不计重力)从P点先后射入磁场,粒子a正对圆心射入,速度方向改变60°后离开磁场,粒子b射入磁场时的速度方向与粒子a射入时的速度方向成60°,已知它们离开磁场的位置相同,下列说法正确的是( )| A. | 磁场的方向垂直纸面向外 | |
| B. | 两粒子在磁场中运动的时间之比为$\frac{{t}_{a}}{{t}_{b}}$=$\frac{1}{3}$ | |
| C. | 两粒子在磁场中运动的速度之比为$\frac{{v}_{a}}{{v}_{b}}$=$\frac{2}{1}$ | |
| D. | 两粒子在磁场中运动的轨迹长度之比为$\frac{{s}_{a}}{{s}_{b}}$=$\frac{1}{2}$ |
 如图甲所示,直线AB是某电场中的一条电场线,若在A点放置一初速度为零的质子,质子仅在电场力作用下,沿直线AB由A运动到B过程中速度随时间变化的图象如图乙所示.则下列说法中正确的是( )
如图甲所示,直线AB是某电场中的一条电场线,若在A点放置一初速度为零的质子,质子仅在电场力作用下,沿直线AB由A运动到B过程中速度随时间变化的图象如图乙所示.则下列说法中正确的是( )| A. | A点的电场强度一定大于B点的电场强度 | |
| B. | 电场一定不是孤立点电荷电场 | |
| C. | 质子从A到B的过程中,在连续相等的时间间隔内,电场力做功的平均功率一定相等 | |
| D. | 质子从A到B的过程中,在连续相等的时间间隔内,电场力的冲量一定相等 |
 质量为m的物体从地面上方H高处无初速度释放,落在地面后出现一个深度为h的坑,如图所示.在不计空气阻力的情况下,对全过程的以下说法中正确的是( )
质量为m的物体从地面上方H高处无初速度释放,落在地面后出现一个深度为h的坑,如图所示.在不计空气阻力的情况下,对全过程的以下说法中正确的是( )| A. | 外力对物体做的总功为零 | |
| B. | 物体的机械能减少mg(H+h) | |
| C. | 地面对物体的阻力对物体做功为-mgH | |
| D. | 地面对物体的平均阻力大小为$\frac{mg(H+h)}{h}$ |
| A. | 中子是英国物理学家查德威克发现的,并因此于1935年获得了诺贝尔物理学奖 | |
| B. | 1847年德国物理学家亥姆霍兹在理论上概括和总结了自然界中最重要、最普遍的规律之一----能量守恒定律 | |
| C. | 我国宋朝发明的火箭是现代火箭的鼻祖,与现代火箭原理相同,但现代火箭结构复杂,其所能达到的最大速度主要取决于向后喷气速度和质量比 | |
| D. | 经典力学有一定的局限性,仅适用于微观粒子和低速运动、弱引力场作用的物体 |