题目内容
11.宇航员在某星球表面让一个小球以v0的速度做竖直上抛运动,经过时间t小球落回到抛出点,万有引力常量为G,若忽略星球自传.(1)求该星球表面附近的重力加速度g;
(2)已知该星球的半径为R,求该星球的密度ρ.
分析 (1)小球在月球表面做竖直上抛运动,由速度时间公式求出月球表面的重力加速度;
(2)忽略球体自转的影响,万有引力和重力相等求解中心天体的质量,再根据$ρ=\frac{m}{V}$求解天体密度.
解答 解:(1)小球竖直上抛后做匀变速直线运动,取竖直向上为正方向,根据运动学规律有:$v={v}_{0}^{\;}+at$
代入数据:$0={v}_{0}^{\;}+(-g)\frac{t}{2}$
解得:$g=\frac{2{v}_{0}^{\;}}{t}$
(2)设某星球的质量为M,忽略星体和地球的自转,表面的物体受到的万有引力等于重力,有:
$G\frac{Mm}{{R}_{\;}^{2}}=mg$
解得:$M=\frac{g{R}_{\;}^{2}}{G}$
该星球的密度为$ρ=\frac{M}{V}$=$\frac{\frac{g{R}_{\;}^{2}}{G}}{\frac{4π{R}_{\;}^{3}}{3}}=\frac{3{v}_{0}^{\;}}{2πGRt}$
答:(1)求该星球表面附近的重力加速度g为$\frac{2{v}_{0}^{\;}}{t}$;
(2)已知该星球的半径为R,求该星球的密度ρ为$\frac{3{v}_{0}^{\;}}{2πGRt}$
点评 解决本题的关键掌握万有引力等于重力这一重要理论,并能灵活运用,该理论运用比较广泛,所以将$GM=g{R}_{\;}^{2}$称为“黄金代换式”

练习册系列答案
相关题目
2.真空中有两个静止的点电荷,他们之间的相互作用为F,若将它们所带电荷量都增大为原来的2倍,距离减少为原来的$\frac{1}{2}$,则它们之间的相互作用力变为( )
| A. | 16F | B. | 8F | C. | 4F | D. | 2F |
6. 如图所示,一个轻杆倾斜放置,杆上固定两个质量相同的小球A和B,绕竖直轴线转动,A和B分别在图示所在的水平面内做匀速圆周运动,则( )
如图所示,一个轻杆倾斜放置,杆上固定两个质量相同的小球A和B,绕竖直轴线转动,A和B分别在图示所在的水平面内做匀速圆周运动,则( )
 如图所示,一个轻杆倾斜放置,杆上固定两个质量相同的小球A和B,绕竖直轴线转动,A和B分别在图示所在的水平面内做匀速圆周运动,则( )
如图所示,一个轻杆倾斜放置,杆上固定两个质量相同的小球A和B,绕竖直轴线转动,A和B分别在图示所在的水平面内做匀速圆周运动,则( )| A. | A球线速度必定等于B球的线速度 | |
| B. | A球对筒壁的压力必定大于B球对筒壁的压力 | |
| C. | A球角速度必定大于B球的角速度 | |
| D. | A球的运动周期必定大于B球的运动周期 |
16.下列哪种情况下,物体会做离心运动( )
| A. | 合力大于向心力 | B. | 合力小于向心力 | C. | 合力等于向心力 | D. | 与受力无关 |
3. 当汽车静止时,车内乘客看到窗外雨滴沿竖直方向OE匀速运动.现从t=0时汽车由静止开始做甲、乙两种匀加速启动,甲种状态启动后t1时刻,乘客看到雨滴从B处离开车窗,乙种状态启动后t2时刻,乘客看到雨滴从F处离开车窗,F为AB的中点.则t1:t2为( )
当汽车静止时,车内乘客看到窗外雨滴沿竖直方向OE匀速运动.现从t=0时汽车由静止开始做甲、乙两种匀加速启动,甲种状态启动后t1时刻,乘客看到雨滴从B处离开车窗,乙种状态启动后t2时刻,乘客看到雨滴从F处离开车窗,F为AB的中点.则t1:t2为( )
 当汽车静止时,车内乘客看到窗外雨滴沿竖直方向OE匀速运动.现从t=0时汽车由静止开始做甲、乙两种匀加速启动,甲种状态启动后t1时刻,乘客看到雨滴从B处离开车窗,乙种状态启动后t2时刻,乘客看到雨滴从F处离开车窗,F为AB的中点.则t1:t2为( )
当汽车静止时,车内乘客看到窗外雨滴沿竖直方向OE匀速运动.现从t=0时汽车由静止开始做甲、乙两种匀加速启动,甲种状态启动后t1时刻,乘客看到雨滴从B处离开车窗,乙种状态启动后t2时刻,乘客看到雨滴从F处离开车窗,F为AB的中点.则t1:t2为( )| A. | 2:1 | B. | 1:$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | 1:($\sqrt{2}$-1) |
20. 平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动.在同一坐标系中作出它们的速率图象如图,则( )
平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动.在同一坐标系中作出它们的速率图象如图,则( )
 平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动.在同一坐标系中作出它们的速率图象如图,则( )
平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动.在同一坐标系中作出它们的速率图象如图,则( )| A. | 图线1表示水平分运动的速率图线 | |
| B. | 图线2表示竖直分运动的速率图线 | |
| C. | t1时刻物体的速度方向与初速度方向夹角为45° | |
| D. | 以上说法都不对 |
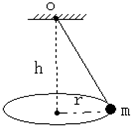 如图所示,在“用圆锥摆验证向心力表达式”的实验中,若测得小球质量为m,圆半径为r,小球到悬点大竖直高度为h,则小球所受向心力大小为$\frac{mgr}{h}$.
如图所示,在“用圆锥摆验证向心力表达式”的实验中,若测得小球质量为m,圆半径为r,小球到悬点大竖直高度为h,则小球所受向心力大小为$\frac{mgr}{h}$. 如图所示,m1和m2是两个质量均匀分布的球体,球心间距离为L,在其连线上有一个质量为m的小球,受到两球的引力,若引力的合力为零,则m到m2的距离为多少?
如图所示,m1和m2是两个质量均匀分布的球体,球心间距离为L,在其连线上有一个质量为m的小球,受到两球的引力,若引力的合力为零,则m到m2的距离为多少?