题目内容
7.质量为m的汽车,在平直公路上以恒定的加速度匀加速启动,汽车到达额定功率时速度的大小v,此时恰好开始下坡,司机立刻调整发动机的功率为额定功率的一半,使汽车以大小为v的速度沿坡路匀速下滑,下滑一段路程后汽车又开足马力以额定功率加速下滑,在坡路上加速t时间后,车速达到最大,且最大车速是刚下坡时速度的2倍.已知坡面的倾角为θ,重力加速度为g,水平路面和坡面对车的阻力相同,在t时间内汽车沿坡路通过的距离为S.试求:(1)汽车的额定功率.
(2)平直公路和坡面对车的阻力的大小.
(3)汽车在平直公路上匀加速行驶的加速度的大小.
分析 (1)汽车在加速下坡的过程中,牵引力、重力和阻力做功,由动能定理即可求出汽车的功率;
(2)汽车匀速下坡的过程中受力平衡,根据受力分析即可求出阻力;
(3)汽车在水平面上运动的过程中合力提供加速度,通过受力分析即可求出加速度.
解答 解:(1)(2)汽车在加速下坡的过程中,牵引力做正功、重力做正功,阻力做负功,由动能定理得:
$Pt+mgsinθ•S-f•S=\frac{1}{2}m(2v)^{2}-\frac{1}{2}m{v}^{2}$ ①
汽车匀速下坡的过程中受力平衡,根据受力分析可知:
$\frac{\frac{P}{2}}{v}+mgsinθ=f$ ②
联立①②得:汽车的功率:P=$\frac{3m{v}^{3}}{2vt-S}$,f=$\frac{3m{v}^{2}}{4vt-2S}+mgsinθ$
(3)汽车在水平面上运动的过程中受到牵引力与阻力的作用,合力提供加速度,由牛顿第二定律得:
F-f=ma ③
又:$F=\frac{P}{v}$ ④
联立以上方程,得:a=$\frac{3{v}^{2}}{4vt-2S}-gsinθ$
答:(1)汽车的额定功率是$\frac{3m{v}^{3}}{2vt-S}$.
(2)平直公路和坡面对车的阻力的大小是$\frac{3m{v}^{2}}{4vt-2S}+mgsinθ$.
(3)汽车在平直公路上匀加速行驶的加速度的大小是$\frac{3{v}^{2}}{4vt-2S}-gsinθ$.
点评 该题结合机车的启动模型,综合考查了动能定理、牛顿第二定律以及瞬时功率与速度的关系等,涉及的知识点比较多,难度中等,需加强这类题型的训练.

练习册系列答案
相关题目
17.在平直的公路上有甲、乙两辆汽车.乙在甲的前方s0处以速度v匀速运动,甲以初速度v′(v′>v)做匀减速运动,试图追赶乙车.则( )
| A. | 甲车一定能追上乙车 | |
| B. | 甲车可能追上乙车后,又被乙车反超 | |
| C. | 甲车的加速度越大,越有可能追上乙车 | |
| D. | 甲车和乙车速度相等时,两车的距离肯定是最大的 |
18. 如图所示,将两个相同的木块a、b置于固定在水平面上的粗糙斜面上,a、b中间用一轻弹簧连接,b的右端用细绳与固定在斜面上的挡板相连.开始时a、b均静止,弹簧处于压缩状态,细绳上有拉力,下列说法正确的是( )
如图所示,将两个相同的木块a、b置于固定在水平面上的粗糙斜面上,a、b中间用一轻弹簧连接,b的右端用细绳与固定在斜面上的挡板相连.开始时a、b均静止,弹簧处于压缩状态,细绳上有拉力,下列说法正确的是( )
 如图所示,将两个相同的木块a、b置于固定在水平面上的粗糙斜面上,a、b中间用一轻弹簧连接,b的右端用细绳与固定在斜面上的挡板相连.开始时a、b均静止,弹簧处于压缩状态,细绳上有拉力,下列说法正确的是( )
如图所示,将两个相同的木块a、b置于固定在水平面上的粗糙斜面上,a、b中间用一轻弹簧连接,b的右端用细绳与固定在斜面上的挡板相连.开始时a、b均静止,弹簧处于压缩状态,细绳上有拉力,下列说法正确的是( )| A. | a所受的摩擦力一定不为零 | |
| B. | b所受的摩擦力一定不为零 | |
| C. | 细绳剪断瞬间,a所受摩擦力变大 | |
| D. | 细绳剪断瞬间,b所受摩擦力不能为零 |
2. 将质量为m甲=1kg、m乙=0.5kg的甲、乙两根条形磁铁放在光滑水平面上,其N极相对,轴线在同一直线上.如图所示,现轻推以下使它们相向运动,某时刻它们的速度大小分别为V甲=2m/s,V乙=3m/s,方向如图,如果两磁铁没有接触就分开了,则以下判断中正确的是( )
将质量为m甲=1kg、m乙=0.5kg的甲、乙两根条形磁铁放在光滑水平面上,其N极相对,轴线在同一直线上.如图所示,现轻推以下使它们相向运动,某时刻它们的速度大小分别为V甲=2m/s,V乙=3m/s,方向如图,如果两磁铁没有接触就分开了,则以下判断中正确的是( )
 将质量为m甲=1kg、m乙=0.5kg的甲、乙两根条形磁铁放在光滑水平面上,其N极相对,轴线在同一直线上.如图所示,现轻推以下使它们相向运动,某时刻它们的速度大小分别为V甲=2m/s,V乙=3m/s,方向如图,如果两磁铁没有接触就分开了,则以下判断中正确的是( )
将质量为m甲=1kg、m乙=0.5kg的甲、乙两根条形磁铁放在光滑水平面上,其N极相对,轴线在同一直线上.如图所示,现轻推以下使它们相向运动,某时刻它们的速度大小分别为V甲=2m/s,V乙=3m/s,方向如图,如果两磁铁没有接触就分开了,则以下判断中正确的是( )| A. | 甲反向时,乙的速度为1m/s,方向不变 | |
| B. | 乙反向时 甲的速度为0.5m/s,方向不变 | |
| C. | 甲、乙相距最近是速度均为零 | |
| D. | 甲、乙相距最近是速度均为$\frac{1}{3}$m/s |
16.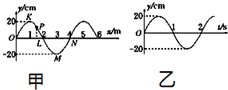 某横波在介质中沿x轴传播,图甲为t=0.25s时的波形图,图乙为P点(x=1.5m处的质点)的振动图象,那么下列说法正确的是( )
某横波在介质中沿x轴传播,图甲为t=0.25s时的波形图,图乙为P点(x=1.5m处的质点)的振动图象,那么下列说法正确的是( )
 某横波在介质中沿x轴传播,图甲为t=0.25s时的波形图,图乙为P点(x=1.5m处的质点)的振动图象,那么下列说法正确的是( )
某横波在介质中沿x轴传播,图甲为t=0.25s时的波形图,图乙为P点(x=1.5m处的质点)的振动图象,那么下列说法正确的是( )| A. | t=0.25s时,质点P正在往负方向运动 | |
| B. | 该波向右传播,波速为2m/s | |
| C. | 质点L与质点N的运动方向总相反 | |
| D. | t=1.25s时,质点K向右运动了2m |
17.下列说法中正确的是( )
| A. | 原子核内部一个质子转化成一个中子时,会同时释放出一个电子 | |
| B. | 裂变物质体积小于临界体积时,链式反应一样能进行 | |
| C. | 电子的衍射现象说明实物粒子也具有波动性 | |
| D. | 235U的半衰期约为7亿年,随地球环境的变化,半衰期可能变短 |
 如图所示,线圈内有理想边界的磁场,开始时磁场的磁感应强度为B0.当磁场均匀减小时,有一带电微粒静止于平行板(两板水平放置)电容器中间,若线圈的匝数为n,平行板电容器的板间距离为d,粒子的质量为m,带电荷量为q.(设线圈的半径为r)求:
如图所示,线圈内有理想边界的磁场,开始时磁场的磁感应强度为B0.当磁场均匀减小时,有一带电微粒静止于平行板(两板水平放置)电容器中间,若线圈的匝数为n,平行板电容器的板间距离为d,粒子的质量为m,带电荷量为q.(设线圈的半径为r)求:


